Wie können wir helfen?
Seit der Mensch die Schrift erfunden hat, konnte das Bedürfnis, Botschaften an andere oder sogar alle Menschen zu richten, befriedigt werden. So unterscheiden wir Geschichte von der Vorgeschichte: Die Geschichte zeichnet sich durch überlieferte Texte gegenüber der Vorgeschichte aus. Texte, die mehr oder weniger erhalten auf uns gekommen sind, liefern uns natürlich wesentlich bessere Informationen als Artefakte, die von der historischen Forschung gedeutet werden müssen. Trotzdem gibt es immer wieder die Notwendigkeit, den richtigen Schlüssel zu finden, ohne die die älteren Texte nicht gelesen werden können. Da ist es natürlich ein großes Glück, wenn man beispielsweise den Schlüssel in einem Dokument findet, das beispielsweise den gleichen Text in zwei oder mehr Sprachen findet, so z.B. die Entzifferung der Hieroglyphen mit dem dreisprachigen Stein von Rosette.
Gerade in Kriegszeiten wollte und musste man Botschaften austauschen, die aber vom Feind – falls sie ihm in die Hände fielen – nicht gelesen werden konnten. Eine der ältesten Verschlüsselungen erfanden wohl die Griechen mit ihrer Skytale.
In der Mathothek gibt es ein vergleichbares Exponat. Es besteht aus drei unterschiedlich dicken Stäben von Bambusrohr, Lederbändern und einem Stift. Einer der beiden Lederriemen trägt auf einer Seite eine völlig unverständliche Folge von normalen Großbuchstaben. Das ist der verschlüsselte Text.
Wickelt man diesen Riemen um den richtigen Stab, so ergeben die untereinander geschriebenen Buchstaben den Klartext. Versucht man dieses Vorgehen mit einem dünneren oder dickeren Stab, so erschließt sich die verschlüsselte Botschaft nicht.
Der Klartext beginnt mit MATHOTHEK … , wie man sehen kann. Den Rest der Botschaft kannst Du in der Mathothek selbst herausfinden.
Natürlich ist diese Verschlüsselung relativ leicht zu knacken, wenn man erkennt, wie die Windungen die Buchstaben auf dem Riemen anordnen. Bei unserem Beispiel sind die entsprechenden Buchstaben jeweils um fünf Plätze verschoben.
Das oben abgebildete Exponat in der Mathothek ist eine nachgebaute Caesarscheibe. Sie ist ebenfalls eine sehr alte Hilfe zur Verschlüsselung von Texten. Ihr Name weist auf den berühmten römischen Feldherren Julius Caesar hin, der sie im Gallischen Krieg als kryptographisches Instrument einsetzte. Sie ist aus zwei konzentrischen Kreisen drehbar zusammengesetzt. Beide Scheiben tragen am Rande jeweils in der normalen Reihenfolge die 26 Buchstaben des deutschen Alphabets, die jeweils denselben Abstand haben.
Das Verschlüsseln des Klartextes mithilfe der Caesarscheibe ist recht einfach: Man wählt zunächst den Verschlüsselungsbuchstaben, z.B. A→E. Man wählt den äußeren Buchstabenkranz für den Klartext und dreht den kleineren so, dass dessen E über dem Klartext A steht. Dann ersetzt man die Buchstaben des Klartextes einen nach dem anderen in den Geheimtext. Nehmen wir als Beispiel den “Geheimtipp” MATHOTHEK so erhalten wir QEXLSXLIO.
Um aus dem Geheimtext wieder Klartext zu machen, nehmen wir den äußeren Buchstabenkranz für die Geheimschrift und den inneren für den Klartext und nehmen den Gegenschlüssel A →W (d.h. E → A).
Stellt man über das A das K des Verschlüsselungsalphabets, so erhält man aus MATHOTHEK das verschlüsselte Wort WKDRYDROU. Wie lautet MATHOTHEK bei der Verschlüsselung A → N?
Die Schlüsselvermittlung ist nicht der einzige Schwachpunkt dieses Codes. Eine gute Möglichkeit ihn zu knacken besteht darin – wenn die zugrunde liegende Sprache bekannt ist – die relative Häufigkeit der Buchstaben zu nutzen. Im Deutschen ist der Buchstabe E weitaus am häufigsten, relative Häufigkeit von E ist 17,40 %. So sucht man den relativ häufigsten Buchstaben des Geheimtextes und stellt diesen Buchstaben versuchsweise über das Klartext E. Dieser Weg ist umso erfolgreicher, je länger der Text ist. Das ist aber nicht die einzige Knackhilfe. Eine weitere Schwäche der Verschlüsselung mit der Caesarscheibe ist es, dass der Gegenschlüssel praktisch mit dem Schlüssel übereinstimmt: Schlüssel A → X, Gegenschlüssel X → A.
Versuche einmal folgenden Geheimtext zu dechiffrieren:
USWKSJ AKL OAW ESF OWAKK FAW AF VWJ ESLZGLZWC YWOWKWF WAYWFLAUDZ KUZSVW GVWJ ?
Die Leerstellen sind natürlich hilfreich.
Das Prinzip der Caesarscheibe spielt in der Kryptographie eine große Rolle, und zwar dadurch, dass man zugunsten der Sicherheit den Schlüssel bei der Verwendung sehr häufig wechselt. Auch der schwer oder gar nicht knackbare Vigènere-Code, geht auf die Caesarscheibe zurück. Das macht natürlich den Schlüsselaustausch aufwendiger und unsicherer.
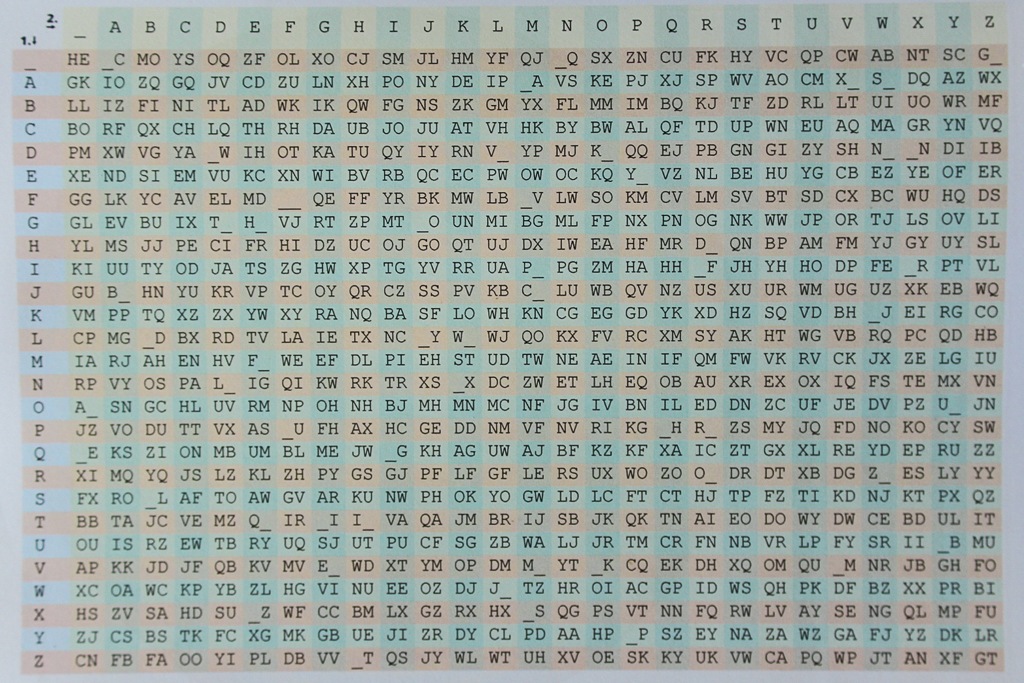
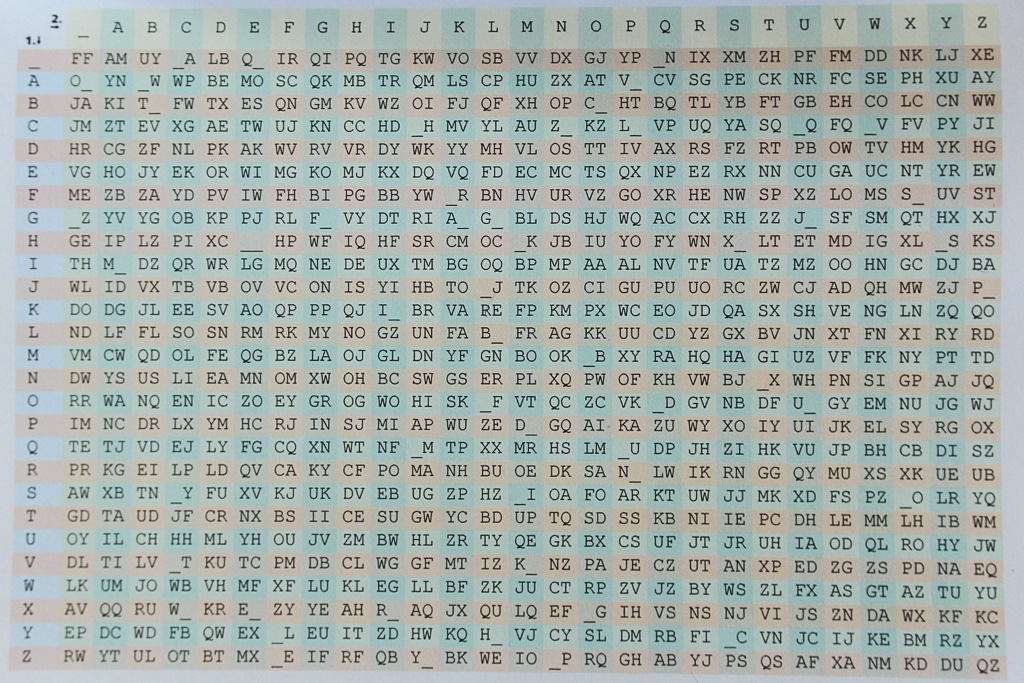
Das zu diesem interessanten Verschlüsselungsverfahren in der Mathothek vorhandene Experiment ist eine Vigènere-Tabelle mit einer Plexiglasscheibe.
Diese Scheibe ist nur eine Hilfe beim Suchen von Schnittpunkten einer Zeile und einer Spalte, um Fehler zu vermeiden. Die Tabelle selbst ist ein lateinisches Quadrat, d.h. in jeder der Zeilen und jeder Spalte befinden sich alle 26 Buchstaben des Alphabets. Die erste Zeile und die erste Spalte sind die beiden Eingänge der Tabelle. In der ersten Spalte suchen wir den Verschlüsselungsbuchstaben auf und damit diejenige Zeile, die den verschlüsselten Buchstaben enthält, und zwar in der Spalte, die mit dem Klarbuchstaben beginnt. Kurz gefasst, findet man den Verschlüsselungsbuchstaben als Schnittpunkt einer Zeile mit einer Spalte. Dabei beginnt die Zeile mit dem Schlüsselbuchstaben und die Spalte mit dem Klartext-Buchstaben.
Hier sind zwei Beispiele:
Im ersten Bild zeigen wir die Verschlüsselung des Buchstabens Q mit dem Schlüssel R: Wir suchen zuerst die R-te Zeile und dann die Q-te Spalte. Der Schnittpunkt ist H, also wird Q in H verschlüsselt.
Im zweiten Beispiel verschlüsseln wir C mit Schlüssel I zu K:
Im dritten Beispiel nehmen wir ERDE als Klarwort und VOGEL als Schlüssel. In der Eingangsspalte suchen wir V, dann suchen wir in dieser Zeile die Verschlüsselung von E, das ist Z, der Schnittpunkt der V-ten Zeile mit der E–ten Spalte. Genauso finden wir im Schnittpunkt der O-ten Zeile mit der R-ten Spalte F als Verschlüsselung von R, ebenso den Schnittpunkt J der G-ten Zeile mit der D-ten Spalte als Verschlüsselung von D und schließlich im Schnittpunkt der E-ten Zeile mit der E-ten Spalte I, die Verschlüsselung von E. Damit wird aus dem Klartext ERDE mit der Verschlüsselung VOGEL der Geheimtext ZFJI. Unten ein Überblick:
| Klartext | E | R | D | E | |
| Schlüssel | V | O | G | E | L |
| Verschlüsselung | Z | F | J | I |
Hier wurden zur Verschlüsselung nicht alle Buchstaben des Schlüssels gebraucht. Wenn der Klartext mehr Buchstaben hat als der Schlüssel, so beginnt man wieder mit dem ersten Buchstaben des Schlüssels. Diese Form der Verschlüsselung ist sehr aufwendig, aber auch sicher. Dazu sollte der Schlüssel nicht zu kurz sein. Hat er mehr Buchstaben als der Klartext, so ist er nicht zu knacken. Tipp: Man nehme z.B. ein langes Gedicht. Oder man bestimme den Schlüssel durch Zufall. Beispielsweise mit folgendem Würfel:
Dieser Würfel hat auf seinen 30 Rauten (Rhomben) die 26 Buchstaben des deutschen Alphabets und vier weitere Leerzeichen. Da dieser Würfel vollkommen symmetrisch ist, lässt sich jeder Schlüsselbuchstabe rein zufällig festlegen. Natürlich muss der zufällig bestimmte Schlüssel sicher übertragen werden. Diesen Würfel findest Du mit einer großen Menge verschiedener weiterer in der reichen Würfelsammlung der Mathothek.
Ein großer Nachteil des Vigènere-Code ist seine Symmetrie, d.h. wer den Schlüssel kennt, kann mit ihm nicht nur entschlüsseln, sondern könnte auch auf dieselbe Weise einen abgefangenen Geheimtext unbemerkt verändern.
Das folgende Objekt der Mathothek ist ebenfalls ein gutes Experiment zur Verschlüsselung von Nachrichten:
Es besteht aus einem Rahmen, einer versteckten Botschaft und einer gelochten Schablone. Die Botschaft ist in einem mit einer anscheinend sinnlosen Verteilung von Buchstaben gefüllten Quadrat versteckt. Um in dem Buchstaben-Durcheinander die Botschaft zu entdecken, benutzt der Empfänger die weiße Schablone.
Liegt diese Schablone richtig auf dem Buchstaben-Wirrwarr, so verdeckt sie alle überflüssigen Buchstaben und in den runden Löchern erscheint die Botschaft: WER IMMER NUR NACH DEM NUTZEN DER DINGE FRAGT WIRD IHRE SCHÖNHEIT NIE ENTDECKEN. Hier ist natürlich der Schlüsselaustausch, der Austausch der Schablone ein wunder Punkt.
Man sieht immer wieder, dass der Austausch von Schlüsseln eine Schwachstelle darstellt. Deswegen gibt es in der Mathothek auch ein einfaches Experiment, wie es prinzipiell auch ohne einen Austausch des Schlüssels funktionieren kann.
Dieses Exponat besteht aus einem Holzkästchen, zwei verschiedenen Vorhängeschlössern, entsprechenden Schlüsseln und einem geheimnisvollen schwarzen Gegenstand. Wir stellen uns zwei Personen A und B vor. A möchte die Kiste mit Inhalt sicher verschlossen an B schicken. Wie lässt sich das machen, ohne dass B den Schlüssel von A bekommt?
A packt die Kiste und verschließt sie mit seinem Schloss und verschickt das Paket an B. Den Schlüssel behält er.
B erhält das verschlossene Paket. Natürlich kann er es nicht öffnen, weil er mit seinem Schlüssel das Schloss von A nicht öffnen kann. Deswegen schließt er mit seinem Schloss und seinem Schlüssel die Kiste sicher ab und schickt sie an A zurück.
A nimmt seinen Schlüssel und entfernt sein eigenes Schloss. Anschließend schickt er das Paket wieder an B, der nun mit seinem Schlüssel an den geheimnisvollen Gegenstand gelangt.
Fazit: Kein Schlüsselaustausch zwischen A und B, das Paket war die gesamte Zeit verschlossen. A und B haben es geschafft. Allerdings musste das Paket zweimal hin und her geschickt werden.
Man kann aber auch einen Text verschlüsseln, indem man für jeden Buchstaben ein neues Zeichen erfindet. Das haben z.B. die Freimaurer so gemacht. Aber auch zwei kleine Mädchen einer fünften Klasse.
Diesen Schlüssel für die geheime schriftliche Kommunikation der beiden Mädchen lag irgendwann vergessen auf dem Klassenboden. Warum auch immer. Und ich fand die Idee der beiden so schön, dass er schon seit mehr als zehn Jahre zu einem sympathischen Exponat der Mathothek aufgestiegen ist.
Für eine ebenfalls sehr einfache Art, privat geheime Nachrichten auszutauschen, kann das folgende Exponat dienen:
Hier handelt es sich darum, dass man nicht neue Zeichen für die Buchstaben des Alphabets erfindet, sondern eine neue Reihenfolge der 26 Buchstaben vereinbart. Auch hier ist zunächst ein Schlüsselaustausch nötig. Die verschlüsselte Kommunikation kann durch entsprechende Buchstabenleisten vereinfacht werden. Die beiden Leistenpaare können als bequemer Schlüssel und Gegenschlüssel dienen.
Unter Schülern gibt es eine stille und wortlose Art der Verständigung: das Fingeralphabet. Es ist ziemlich umständlich, aber wird oft von den Lehrern deswegen nicht wahrgenommen. In der Mathothek gibt es eine Anleitung. Damit ist das Finger-ABC ein öffentlicher Schlüssel, d.h. jeder kann sich hier beteiligen, wenn er will und sich den Code aneignet. Dagegen ist das vorige Geheimalphabet ein privater Schlüssel, dessen Reiz es ausmachte, dass sich hier nur die beiden Schlüsselbesitzerinnen verständigen konnten – bis er in der Mathothek als reizvolles Exponat öffentlich wurde.
Es gibt viele Verschlüsselungen, die nicht zur Geheimhaltung einer Botschaft dienen, sondern aus anderen Notwendigkeiten heraus entwickelt wurden, so z.B. das Morse-Alphabet. Dabei handelt es sich um eine binäre Codierung des ABCs mithilfe von verschiedenen Kombinationen zweier Zeichen: kurz = . und lang = – ! Auch hierzu gibt es ein Angebot in der Mathothek:
Die Kärtchen tragen auf der einen Seite den entsprechenden Buchstaben und auf der anderen das dazugehörige Morsezeichen.
Hier stand die technische Möglichkeit der schnellen und über große Entfernungen erfolgenden Übermittlung mittels eines Telegrafen im Hintergrund. Eine weitere Codierung des Alphabets mit einem für jeden zugänglichen Schlüssel ist die Brailleschrift für Blinde.
Diese Blindenschrift benutzt fühlbare Punkte, die in einem 2×3-Schema verschieden angeordnet werden können. Natürlich gibt es hierzu ein Exponat in der Mathothek, mit dem Sehende ebenso wie Sehbehinderte experimentieren und ein Stück Kombinatorik erfahren können:
Das nächste Bild zeigt noch ein kleines aus Bauteilen zusammengesetztes Objekt, das man gut zum Verschlüsseln von Zahlen verwandt werden kann. Eine Schlüsselzahl an der richtigen Stelle, die durch Pfeile gekennzeichnet ist, erlaubt die Ver- und Entschlüsselung der gewünschten Zahlen.
Für die Entwicklung der Kryptographie spielte und spielt das Prinzip der Caesarscheibe eine ganz wichtige Rolle. Außerdem geht es immer wieder um die Frage der Schlüsselsicherung. Zu dem Thema der Verschlüsselung gibt es noch einige interessante Experimente in der Mathothek, z.B. ein asymmetrisches Verfahren mit privatem und öffentlichem Schlüssel:
Sehr sicher ist die Verschlüsselungsmethode des “Versteckens”, bei der der Gegner gar nicht weiß, wo er die Geheimbotschaft überhaupt suchen soll. Oder kannst Du in dem folgenden Brief die versteckte Mitteilung erkennen?
Lieber Klaus, obwohl man mir eintrichterte, mit originellem Rock zu gehen, entschied ich mich nicht dafür.
Kannst Du die geheime Mitteilung erkennen?
Dazu schau Dir die Anfangsbuchstaben der einzelnen “harmlosen” Worte an: LKOMMEMORZGEIMND.
Welche Botschaft versteckt sich wohl hinter dieser E-Mail?
Keine Oma mag mich einladen. Habe einen unfreundlichen Tag erlebt.
Wenn Du auch eine gute Idee für eine versteckte Botschaft hast, kannst Du gerne damit in die Mathothek kommen.