Wie können wir helfen?
Glücksrad, Würfelsammlung, Urne mit Kugeln und Ziehungsgerät sind die beliebtesten Geräte in der Mathothek, um den Zufall zu simulieren:
Verkleinerte Modelle von klassischen Glücksspielen – Roulette und Lotto “Sechs aus 49 mit Zusatzzahl” sind in der Mathothek vorhanden. Auch der fast regelmäßige Begleiter des Glücks, der Betrug, ist in der Mathothek u.a. in Form von gezinkten Würfeln vertreten:
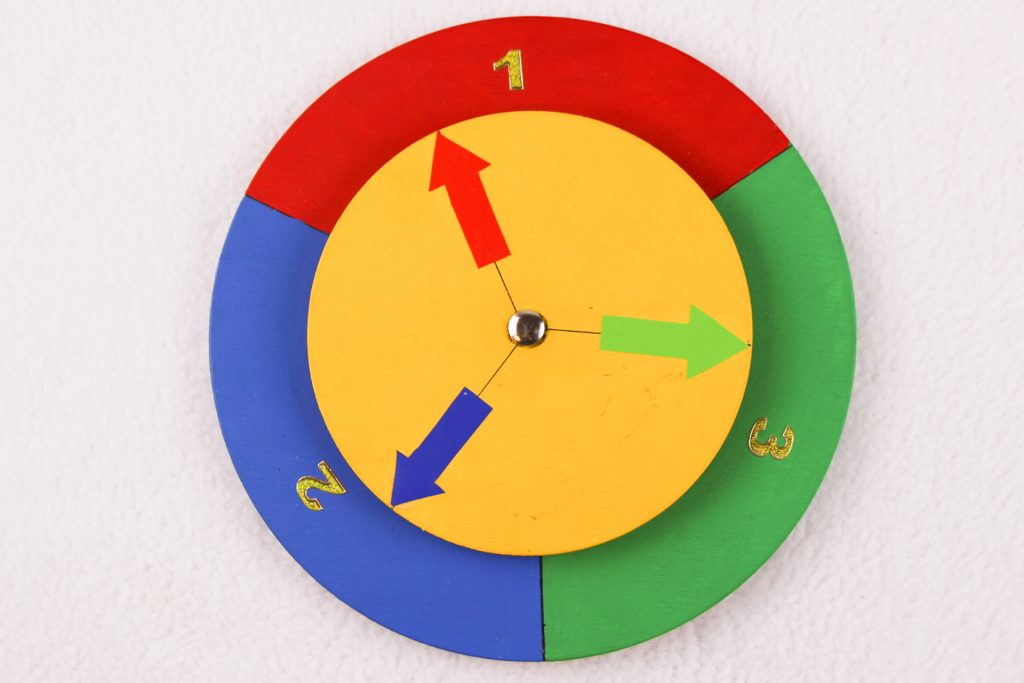
Ein besonders gutes Einstiegsexperiment in die Wahrscheinlichkeitsrechnung ist das folgende Glücksrad:
Es ist für zwei Spieler gedacht. Kennt einer der beiden Kontrahenten sich auch nur in den einfachsten Grundlagen der Wahrscheinlichkeitsrechnung aus, so kann er, als Zweiter seine Chance zu gewinnen, verdoppeln.
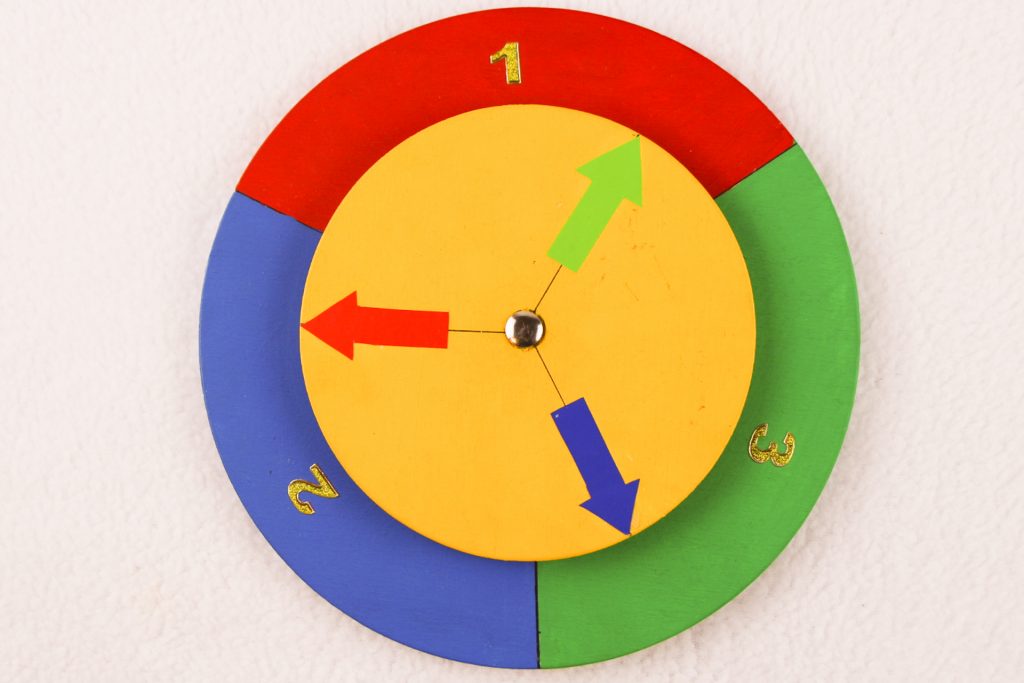
Die Spielregeln sind einfach. Spieler I setzt auf eine der Farben der drei Pfeile: rot, grün oder blau. Dann wählt Spieler II aus den beiden verbliebenen Pfeilen seine Farbe. Das Rad wird in Drehung versetzt. Gewonnen hat der, dessen Pfeil auf die höhere Zahl zeigt.
Das sieht erstmal recht zufällig und gerecht aus, scheint eher vorteilhaft für Spieler I. Tatsächlich kann aber der Zweite seine Chancen verdoppeln. wenn er sich konsequent für den gegen den Uhrzeigersinn befindlichen Pfeil entscheidet. In diesem Fall gewinnt Spieler II in zwei möglichen Ausgängen des Experiments und verliert nur in einem. Davon kann man sich leicht am obigen Beispiel überzeugen.
Reine Glücksspiele beruhen auf purem Zufall. Das einzige Instrument, um hier sichere Aussagen zu machen, ist die mathematische Berechnung von Wahrscheinlichkeiten.
Wie der Titel eines der bekanntesten und verbreitetsten Glücksspiele, nämlich Mensch ärgere Dich nicht, empfiehlt, sollte man sich bei allen Glücksspielen verhalten. Den Zufall, Glück oder Pech, darf man nicht dazu benutzen, um sich schuldig zu fühlen. Schuldig wird man nur, wenn man sich auf Glücksspiele mit echten Risiken gegen alle Vernunft einlässt.
In der Mathothek gibt es ein reines Glücksspiel, das uns eine physikalische Grunderkenntnis über unseren Kosmos veranschaulichen kann: Das Entropiespiel:
Die Spielregeln sind im entsprechenden Artikel ausführlich beschrieben. Aufgrund der Wahrscheinlichkeitsrechnung werden es zunächst immer mehr schwarze Chips auf dem Brett, und zwar bis etwa zur Hälfte, um die die weiteren Spielrunden dann pendeln.
Das bekannte Dominospiel hat nur eine reine Zufallskomponente, das ist die Verteilung der Dominosteine, der eigentliche Spielverlauf ist dann rein strategisch und von unverschuldetem Pech oder Glück kann nicht mehr die Rede sein.
Fast alle Menschen wissen, dass sie ihre Zukunft nicht sicher vorhersehen können. Bei sehr vielen besteht jedoch der große Wunsch, doch eine Antwort darauf zu bekommen, was die eine oder andere Frage im Hinblick auf ihre Zukunft betrifft. Hier werden dann seit jeher gefährliche Wege beschritten: Wahrsagerei, Orakelbefragung und andere Irrationalität.
Ein sehr beliebtes Orakel ist in der Mathothek das folgende Objekt:
Dieses Orakelobjekt ist ein Pendel mit einer schwingenden magnetischen Kugel über einem Kreis mit sechs gleich großen Kreisteilen, in denen die Antworten:YES, NO, TAKE THE RISK, NOT RIGHT NOW, SLEEP ON IT, SEE YOUR THERAPEUT. Der Mathotheksbesucher stellt seine Zukunft betreffende Frage und lässt vom Kreismittelpunkt aus die Kugel los. Die Kugel wird bei einer der sechs möglichen Antworten halten. Natürlich durchschauen alle sehr schnell den “Zauber” und daher ist das Spiel ungefährlich, ja durchaus aufklärend.
Andererseits führte dieses Wissenswollen aber auch zu der Mathematik des Zufalls, der Wahrscheinlichkeitsrechnung. Zusammen mit der Statistik wurde sie zu einem wichtigen und fruchtbaren Gebiet rationalen Umgangs mit der Zukunft.
Die Diskussion, ob das “Spiel des Lebens” nun mehr einem Glücksspiel oder einem strategischen Spiel gleicht, würde wohl den Rahmen dieses Artikels doch ein wenig sprengen. Das “Spiel des Lebens” ist sicher kein reines Strategiespiel, schon gar nicht mit einer sicheren Gewinnstrategie, aber sicher auch kein reines Glücksspiel. In Abwandlung einer bekannten Weisheit hilft vielleicht die Spielstrategie für dieses Glücksspiel: Ändere, was du ändern kannst. Mache das Beste aus dem, was du nicht verändern kannst. Nutze deinen Verstand, um jeweils zu erkennen, was du und wie du es zu tun hast. Und suche dir geeignete Mitspieler.
Dass wir Menschen aber oft Experimente für Zufallsversuche halten, die es aber nicht sind, sondern streng deterministisch, liegt an deren chaotischem Verhalten: Geringste Abweichungen vom Start führen zu enormen Unterschieden im Ergebnis, sodass uns keine Voraussagen mehr möglich sind.
Nachdenklich mag auch mancher Besucher der Mathothek werden, wenn er sich dort mit zwei bunten Perlenketten beschäftigt:
Die beiden Ketten sind offensichtlich nicht identisch, aber doch sehr ähnlich: gleich große Perlen, zehn verschiedene Farben, anscheinend völlig zufällige Reihenfolge. Ordnet man aber den zehn Farben eine bestimmte Zahl von 0 bis 9 zu, so bildet die linke Kette die ersten Nachkommastellen der Zahl π ab. Die Reihenfolge der Farben der anderen Kette entstand durch ein Zufallsgerät:
Weitere und vertiefende Darstellungen zu diesen und ähnlichen Objekten gibt es in weiteren Artikeln des Mathothekskatalogs.