Mathothek

• 

• 

Das “Spiel des Lebens” oder kurz “Life” von “Game of Life” genannte Spiel wurde in den 1970er Jahren von dem englischen Mathematiker John Conway erdacht. Diesem Spiel liegt ein potenziell unendliches Raster aus kleinen Quadraten zugrunde, die Zellen genannt werden. Diese Zellen erwachen zum Leben, leben weiter oder sterben. Das Ganze erfolgt mithilfe von einfachen Regeln und Konfigurationen aus blauen Spielfiguren.

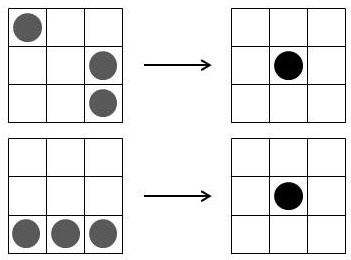
Jede Zelle enthält entweder eine solche blaue Spielfigur, oder sie ist leer. Die blaue Figur bedeutet, dass diese Zelle lebt. In jedem Stadium oder jeder Generation bildet der Satz Spielfiguren eine “Konfiguration”. Die 0. Generation (Startgeneration) verändert sich aufgrund nur weniger Regeln zur ersten Generation. Aus jeder Generation entsteht nach immer denselben vier Regeln die nächste Generation. So entstehen aus der Konfiguration der 0. Generation Schritt für Schritt alle Folgegenerationen. Was mit jeder Zelle passiert, hängt nur von ihren acht unmittelbar benachbarten Zellen ab. Alle Geburten oder Sterbefälle erfolgen gleichzeitig. Die Konfiguration der (n+1). Generation folgt regelmäßig nur aus der Konfiguration der n. Generation.

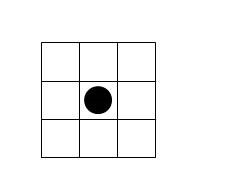
Im Folgenden werden jetzt die vier Regeln genannt und erklärt. Danach erfolgt ein relativ einfaches Beispiel. Die vier Regeln beziehen sich auf jede einzelne Zelle bezüglich ihrem Geborenwerden, Sterben oder Weiterleben, worüber einzig und allein ihre acht Nachbarzellen entscheiden. Hier das Beispiel einer lebenden Zelle mit ihren acht Nachbarzellen:

• 

Regel 1: Wenn eine Zelle lebt und zwei oder drei Nachbarn hat, dann lebt sie auch in der nächsten Generation noch.

• 

Regel 2: Falls die belebte Zelle vier oder mehr Nachbarn hat, stirbt sie und ist in der nächsten Generation nicht mehr da.

• 

Regel 3: Wenn eine belebte Zelle nur höchstens eine belebte Nachbarzelle hat, so stirbt sie und ist in der nächsten Generation nicht mehr da.

• 

Regel 4: Falls eine unbelebte Zelle genau drei belebte Nachbarzellen hat, erwacht sie zum Leben und existiert in der nächsten Generation.

• 

Was mit den anderen acht Zellen passiert, die unsere “Mittelpunktzelle” umgeben, entscheiden allein ihre acht Nachbarzellen aufgrund der vier Regeln.

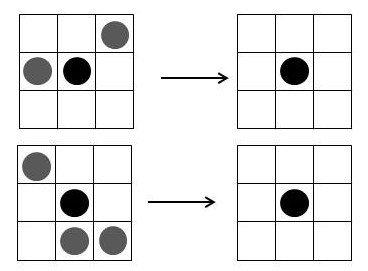
Es folgt ein erstes Beispiel: “Blinker”

• 

• 

Links ist die Ausgangskonfiguration (0. Generation) zusehen: drei blaue Spielfiguren, die senkrecht untereinander angeordnet sind. Blaue Spielfigur bedeutet von jetzt ab, dass diese Zelle lebt. Rechts daneben ist die Konfiguration der 1. Generation zu erkennen: Die obere und die untere lebende Zelle der 0. Generation sterben nach Regel 3 ab, sind in der ersten Folgegeneration nicht mehr vorhanden. Die beiden unbelebten Zellen der 0. Generation links und rechts neben der mittleren belebten Zelle erwachen zum Leben, da sie jeweils drei belebte Nachbarzellen besitzen (Regel 4).

• 

• 

In der 2. Generation erscheint wieder die Konfiguration der 0. Generation, und in der 3. Generation erkennen wir wieder die der 1. Generation., usw.

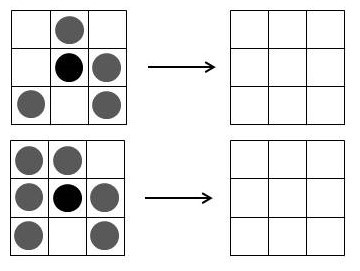
Wie verläuft die “Generationengeschichte” des zweiten Beispiels?

• 

Zunächst erwachen die vier unbelebten Nachbarzellen der mittleren lebenden Zelle zum Leben (Regel 4), dann sterben alle fünf Zellen der 0. Generation ab (Regel 2 und Regel 3). Damit sieht die Konfiguration der 1. Generation so aus:

• 

In der ersten Generation entsteht kein neues Leben, weil keine leere Zelle genau drei lebende Nachbarzellen besitzt (Regel 2, 3 und 4)). Aber es stirbt auch keine, da jede lebende Zelle zwei lebende Nachbarzellen besitzt. Damit ändert sich diese Konfiguration nun von an nicht mehr. 

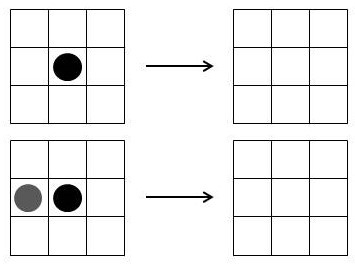
Noch ein Beispiel:

• 

• 

• 

• 

• 

• 

Die Konfiguration der 0. Generation  stirbt nach drei Veränderungen in der 4. Generation aus.

Und hier ein weiteres Beispiel, das nach acht Generationen periodisch endet:

• 

• 

• 

• 

• 

• 

• 

• 

• 

• 

• 

Ab jetzt alternieren die Konfigurationen der 9. und der 10. Generation periodisch. Dennoch zeigt dieses Beispiel, wie die einfachen Regeln des Conway-Spiels aus einfachen Strukturen recht komplexe hervorbringen können.

Dass eine Konfiguration sich unendlich bewegt, das ist nicht so ohne weiteres nachzuweisen. Falls eine Figur irgendwann stirbt oder sich periodisch wiederholt, so wird man – zumindest prinzipiell –  darauf stoßen. Dass egal nach wie vielen Generationen keiner dieser Zustände eintritt, ist natürlich keinerlei Beweis dafür, dass sie unsterblich ist. Mit der Konfiguration des Gleiters gelang zum ersten Mal der Nachweis, dass eine Figur im Spiel des Lebens “ewig” leben kann. Zwar sieht nach wenigen Generationen das Ergebnis immer wieder gleich aus, aber der Gleiter befindet sich weiter rechts unten.

• 

• 

Die große Vielfalt der möglichen Entwicklungen einerseits und das Fehlen jeder offensichtlichen Beziehung zwischen der Anfangsfiguration und der daraus folgenden Entwicklung andererseits machen dieses “Spiel des Lebens” so interessant. Das Regelsystem selbst ist völlig deterministisch, weil die gesamte weitere Entwicklung des Spiels bereits implizit in seinem Anfangszustand steckt. So ist das Spiel eine überzeugende Demonstration für den Unterschied zwischen Determinismus und Vorhersagbarkeit.

Aus mathematischer Sicht liegt es nahe, Spielkonfigurationen nach ihrem Langzeitverhalten einzuteilen. So können Konfigurationen:

1. völlig verschwinden (=aussterben)
2. sich nicht mehr verändern (=Stasis)
3. dieselbe Generationsfolge wiederholen (=Periodizität)
4. dieselbe Folge ständig wiederholen, aber jedes Mal an einer anderen Stelle enden
5. sich chaotisch verhalten
6. sich wie ein Computer verhalten (=universelle Turingmaschine)

Je komplexer die Figuren werden, umso unübersichtlicher und fehleranfälliger wird der Aufbau der nächsten Generation. Als Abhilfe bietet das Exponat der Mathothek auch gelbe und schwarze Spielfiguren an. Es empfiehlt sich folgendes Vorgehen:

1. Man sucht diejenigen Zellen, die neues Leben hervorbringen und kennzeichnet sie jeweils mit einer gelben Spielfigur.
2. Die blauen Spielfiguren in den Zellen, die absterben und in der nächsten Generation nicht mehr vorhanden sind, werden durch schwarze Spielfiguren ersetzt.
3. Nach sorgfältiger Überprüfung wird die Konfiguration hergestellt, indem man die schwarzen Figuren entfernt und die gelben durch blaue austauscht.

Auch hier ein Beispiel:

• 

• 

• 

• 

• 

Damit ist das Endstadium erreicht. Diese “Kreisfigur” kann sich nicht mehr verändern, weil keine Zelle neu zum Leben erwacht, und auch keine Zelle stirbt.

Klar, dass sich “Game of Life” auch programmieren lässt. Dann vermittelt dieses Spiel neben erstaunlichen Einblicken auch viel Vergnügen. Trotzdem ist das Exponat in der Mathothek zum Verständnis hervorragend geeignet.