Wie können wir helfen?
Schach kommt aus dem Persischen, und zwar von Schah, also König. Daher leitet sich auch die Benennung des Schachspiels als “königliches Spiel” ab. Schach ist ein strategisches Brettspiel, bei dem das Spielbrett in 8×8=64 gleich große quadratische Felder unterteilt ist. Diese Felder sind abwechselnd hell oder dunkel gefärbt. Die beiden gegnerischen Spieler bewegen abwechselnd ihre Schachfiguren genannten Spielsteine nach festen Zugregeln auf dem Schachbrett. Es gilt dabei, den Gegner schachmatt zu setzen, das bedeutet, dessen König so anzugreifen, dass diesem weder Abwehr noch Flucht möglich sind.

Schach ist über die ganze Welt bekannt und kulturell verankert. Auch wenn bei weitem nicht jeder aktiv Schach spielt, darf man doch ein gewisses “Schachwissen” wohl zum “Allgemeinwissen” zählen. Inzwischen ist Schach sogar vom Internationalen Olympischen Komitee als Sport anerkannt worden. Viele Schachspieler sind Mitglieder eines Schachvereines. Diese gehören regionalen und nationalen Schachverbänden an, die sich weltweit im Weltschachbund (FIDE) zusammengeschlossen haben. Schachvereine oder Schachverbände, aber auch private Veranstalter organisieren Schachturniere. Frauen können gemeinsam mit Männern an Turnieren teilnehmen oder auch an eigenen Wettkämpfen spielen. An vielen Schulen gibt es als Angebot Schach-AGs.
In der Mathothek gibt es mehrere Schachbretter und auch mehrere Schachfigurensätze:


Go ist ein Brettspiel für zwei Spieler. Das Spiel stammt ursprünglich aus dem alten China und hat sich im Laufe seiner Geschichte auch in Japan und Korea ausgebreitet. In diesem Teil der Welt geniest Go einen vergleichbaren Status wie Schach im Westen. Der Der Name bedeutet wörtlich übersetzt “Umzingelungsspiel” und es gilt als das komplexeste Strategiespiel der Welt. Außerhalb Ostasiens hat sich Go erst seit dem späten 19. Jahrhundert verbreitet. Unter den westlichen Ländern gibt es in Deutschland die meisten Go-Spieler.
Hier ein originales Go-Spiel, das der Mathothek von Frau Dr. Knoche als Leihgabe zur Verfügung gestellt wurde:


Die beiden Spieler setzen abwechselnd flache runde Spielsteine auf die Schnittpunkte der Spielfeldlinien eines 19×19-Bretts und versuchen sog. Gebiete abzugrenzen, diese zu sichern und dabei auch noch Spielsteine des Gegners gefangenzunehmen. Am Ende des Spieles wird die Größe der eigenen Gebiete und die Anzahl der Gefangenen addiert. Es geht also nicht darum, den Gegner zu vernichten, sondern mehr Punkte zu sammeln.

Go ist auf der einen Seite aufgrund der riesigen Anzahl der Spielzüge so komplex, dass man ein Leben lang an der Verbesserung seines Stils und seiner Spielstärke arbeiten kann. Aber andererseits sind die vier Grundregeln so einfach, dass man schon nach einer kurzen Einführung zu spielen beginnen kann. Die besondere Herausforderung von Go besteht darin, dass man jederzeit die lokalen Situationen als immer auch die gesamte Situation im Auge behalten sollte. Außerdem können unterschiedliche Spielstärken durch die Vorgabe bis zu neun Vorgabesteine ausgeglichen werden.
Beim Go-Spiel geht es aber nicht nur um die Technische Beherrschung des Spiels. Es spiegeln sich auch charakterliche Züge der Spieler wider. So kann eine gut gespielte Partie durchaus als “Kunstwerk” sein.
Ähnlich wie beim Schach gibt es auch bei Go Vereinigungen und Turniere.
In der Mathothek gibt es für interessierte Besucher ein Buch Go für Einsteiger und ein kleineres Spielbrett mit den zugehörigen schwarzen und weißen runden Spielsteinen.

Hier das Foto einer Übungsaufgabe:

Die beiden großen Strategiespiele Schach und Go spielen eine wichtige Rolle im Zusammenhang mit der Forschung zur künstlichen Intelligenz. So war mit der Entwicklung des Computers das Schachspiel immer eine Herausforderung, seine Leistungsfähigkeit auch an seiner Fähigkeit zu messen, wie gut er sich gegen den Menschen als Schachspieler behaupten konnte. Und zwar inzwischen mit überwältigendem Erfolg. Allerdings beruht dieser Erfolg vor allem auf seiner wahnsinnigen Schnelligkeit, Möglichkeiten zu berechnen und zu bewerten. Inzwischen scheint hier das wesentlich komplexere Go-Spiel das Schachspiel abzulösen. Grundgedanke ist jetzt nicht mehr, auf die unglaublichen Rechenfähigkeiten des Computers zu setzen, sondern ihn mit den Spielregeln des Go zu füttern und ihn dann gegen sich selbst spielen zu lassen. Mit dem Ziel, dass er mit entsprechenden Belohnungssystemen immer besser und besser wird und den menschlichen Spieler immer häufiger schlagen wird.
In der Mathothek gibt es ein sehr faszinierendes Experiment zum Thema “Computer gegen Mensch”, nämlich den lernenden Computer mit dem Bauernschach:

Hierbei handelt es sich um eine sehr einfache Variante des Schachspiels. Drei rote und drei blaue Bauern stehen sich auf einem 3×3-Brett gegenüber. Ihre möglichen Bewegungen und Schlagmöglichkeiten sind dieselben wie beim normalen Schach. Der große Reiz dieses Bauernschachs besteht darin, dass es sich um ein einfaches Strategiespiel mit einer sicheren Gewinnstrategie für den zweiten Spieler und vollständig Kenntnis aller Spielsituationen handelt. Durch schrittweise Elimination jeder falschen Zugmöglichkeit des Computers wird die Wahrscheinlichkeit, dass der Computer gewinnt, mit jeder Spielrunde größer. Mit jedem Spiel wird der Computer somit besser und wird schließlich gegen jedes menschliche Gegenüber gewinnen. Mehr Informationen gibt es in einem eigenen Artikel.
Mit Chex können interessierte Besucher in der Mathothek eine kleinere, schnellere und aggressivere Variante des Schachspiels kennenlernen. Das Schachbrett besteht bei Chex nicht aus Quadraten in zwei Farben, sondern aus einer bienenwabenartig angeordneten Struktur von regelmäßigen Sechsecken in drei Farben. Bei Chex werden nur fünf Schachfiguren benutzt: König, Läufer, Springer, Turm und Bauer. Auch einige andere Begriffe des normalen Schachspiels werden für Chex entsprechend abgewandelt definiert.

Die Sechsecke des Chexspiels sind beim Spielbrett in der Mathothek aus Herstellungsgründen durch Kreise ersetzt:

Bei Chex gibt es neun weiße und neun schwarze Figuren, und zwar je einen König, einen Springer, einen Läufer und einen Turm. Dazu besitzt jede Partei je fünf Bauern. Die Ausgangsstellung der neun Chex-Figuren sieht dann auf dem Chexbrett folgernder Maßen aus:

Beim Schach unterscheidet man zwischen geradem und schrägem Zug. Für Chex bedeutet ein gerader Zug, dass die Figur von ihrem alten Stand auf einen der sechs benachbarten Kreise ziehen kann (rote Pfeile). Bei einem schrägen Zug kann die Figur zwischen zwei benachbarten Kreisen hindurch auf den diese beiden Kreise berührenden Kreis bewegt werden (weiße Pfeile).

Darf die Figur bei einem geraden Zug nur nach vorne ziehen, so darf sie sich nur in Richtung der gegnerischen Ausgangsstellung bewegen. Also bleiben von den sechs möglichen geraden Zügen nur noch drei und von den sechs möglichen schrägen Zügen Zügen nur noch drei.
Für die fünf Chex-Figuren gelten folgende Regeln:
Der Turm:
Der Turm bewegt sich in gerader Richtung mit beliebiger Anzahl von Schritten und schlägt auch so. Allerdings ist das bei Chex in sechs verschiedenen Richtungen möglich. Damit ist der Turm bei Chex – weil die Dame fehlt – die stärkste Figur.
Der Läufer:
Der Läufer bewegt sich in schräger Richtung mit beliebiger Anzahl von Schritten und schlägt auch so. Auch ihm stehen bei Chex sechs verschiedene Richtungen zur Verfügung. Beim normalen Schach kann sich der Läufer während seines gesamten Einsatzes nur auf Feldern bewegen, die dieselbe Farbe wie das Feld seiner Grundstellung haben. Also sind ihm nur die Hälfte der Felder zugänglich. Bei Chex gilt das auch, aber wegen der drei Farben stehen ihm bei Chex nur ein Drittel der Felder zur Verfügung.
Der Springer:
Der Springer bewegt sich jeweils mit einem geraden und einem schrägen Zug und schlägt auch so. Einerseits kann der Springer so von einem Feld in einem Zug auf ein anderes Feld bewegt werden, wie es keine andere Figur kann. Allerdings ist er durch die Beschränkung auf nur zwei Richtungen und den einen Doppelzug geschwächt. Bei der Kleinheit des Spielbretts ist die zweite Einschränkung nicht ganz so schlimm.
Der Bauer:
Der Bauer kann sich immer nur nach vorne bewegen, und zwar immer nur um ein Feld in gerader Richtung. Schlagen kann der Bauer nur mit einer einzigen schrägen Bewegung, ebenfalls auch nur nach vorne. Nur in seiner Grundstellung hat er dabei bis zu drei Möglichkeiten. Außerhalb seiner Grundstellung entfällt für ihn die mittlere. Der beim klassischen Schach mögliche Doppelzug aus der Grundstellung entfällt bei Chex:

Der König:
Der König kann sich einen Schritt in gerader oder mit beliebig vielen Schritten in schräger Richtung bewegen, allerdings auch in alle sechs Richtungen. Ist das Feld besetzt, so schlägt der König diese Figur.
Wie beim normalen Schach gibt es auch bei Chex noch Extraregeln.
- Wenn ein Bauer die gegnerische Grundlinie erreicht hat, kann er in eine andere beliebige Figur umgewandelt werden.
- Zwei Bauern derselben Farbe, die nebeneinander stehen, sind eine Durchgangssperre für König und Läufer.
- Um zu gewinnen, muss man ihn nicht mattsetzen. Es reicht auch, wenn man alle seine Mannen geschlagen hat.
- Bei Chex gibt es auch eine Rochade, sie funktioniert wie beim klassischen Schach. Vorausgesetzt, dass König und Turm bisher noch nicht bewegt wurden, so darf der Turm einen Schritt nach links bewegt werden und gleichzeitig der König über den Turm springend dessen bisherigen Platz einnehmen. Allerdings darf der König auf keinem der drei beteiligten Felder bedroht sein.
Der Erfinder dieser Variante des Schachspiels war der Architekt und Spiele-Erfinder Edelbert Wiedmann. Seine Inspirationen zu dieser Spielform des klassischen Schachs mit halber Mannschaft und ungewöhnlichem Spielbrett holte er sich aus der vermutlichen oder auch tatsächlichen Entwicklung des “königlichen Spiels”. Die ausführliche Beschreibung dieses Schachspiels mit seinem eigenen Reiz entdeckte ich in einem Artikel von Christoph Pöppe in “Spektrum der Wissenschaft” August 2007.
Es gibt in der Mathothek noch weitere Objekte und Herausforderungen, bei denen es um bestimmte Aspekte des Schachspiels geht.
Unter den “Brettspielen aus aller Welt”, die in der Mathothek vorhanden sind, gibt es eine weitere Variante zum klassischen Schach, die “Der Maharadscha und die Sepoys” genannt wird:

In diesem Spiel für zwei Personen, das auf einem Schachbrett mit allen weißen Figuren (=Sepoys=Soldaten) einerseits und allein mit dem schwarzen König (=Maharadscha) auf der anderen Seite gespielt wird, gelten für die weißen Figuren dieselben Zug- und Schlagregeln wie beim normalen Schach. Allerdings darf der schwarze König auf einem beliebigen, freien Feld platziert werden und sich sowohl wie eine Dame als auch wie ein Springer bewegen. Setzt der Maharadscha den weißen König matt oder setzen die weißen Figuren den Maharadscha matt, ist das Spiel beendet. Wenn Weiß nie eine Figur ungeschützt lässt, gewinnt es. Da der schwarze König sehr beweglich ist, besteht bei jedem Fehler bei Weiß die Möglichkeit für den Maharadscha. den weißen König in die Enge zu treiben.
Springer und magisches Quadrat: Bei diesem Exponat der Mathothek sind ein 8×8-großes magisches Quadrat und ein Springer mit seiner typischen Bewegung auf einem Schachbrett verknüpft: Die Zahlen von 1 bis 64 des (magischen) Quadrates sind so verteilt, dass
- der Springer Zug um Zug alle Zahlen in ihrer natürlichen Anordnung genau einmal erreichen kann.
- die Zahlen von 1 bis 64 so verteilt sind, dass die Zahlen in jeder Zeile, jeder Spalte und jeder Diagonalen immer dieselbe Summe ergeben, nämlich die magische Konstante 260.
Acht-Damen-Problem: Es handelt sich hier um ein ziemlich frühes Objekt in der Mathothek und besteht aus einem großen Schachbrett und acht Dame-Figuren.

Die “schachmathematische” Aufgabe besteht hier darin, dass die acht Damen so auf das Schachbrett platziert werden müssen, dass keine der Damen eine andere schlagen kann. Dazu muss man kein Schachmeister sein, sondern wissen, dass die Damen beim Schach als stärkste auf dem Schachbrett sich geradeaus und schräg in jede Richtung beliebig weit bewegen und auch entsprechend schlagen kann.
Hier ist das Bild einer Lösung des Acht-Damen-Problems:

Die mathematische Seite führt zu kombinatorischen Fragestellungen und ist recht breit bearbeitet worden. Man ignoriert dabei die Figurenfarbe und geht davon aus, dass jede Dame jede andere Dame schlagen könnte. Konkret bedeutet das, es dürfen keine zwei Damen auf derselben waagrechten oder senkrechten Reihe stehen und auch nicht auf derselben Diagonalen.
Insgesamt gibt es 92 Möglichkeiten, das Damenproblem auf einem 8×8-Brett zu lösen. Betrachtet man Lösungen, die sich nur durch eine Spiegelung oder Drehung unterscheiden, so bleiben nur noch 12 Lösungsmöglichkeiten übrig. Unten sind drei Fotos, die verschiedene Lösungen des Acht-Damen-Problems zeigen, die aber durch Spiegelung oder Drehung der Damenstellungen ineinander überführt werden können:



Natürlich hat man dann die Untersuchungen auf beliebige nxn-Bretter mit n Damen erweitert.
Überraschend ist für viele die Antwort auf die Frage, wie viele Möglichkeiten es gibt, eine maximale Anzahl Springer auf einem Schachbrett so zu verteilen, dass keiner von ihnen einen anderen schlagen kann. Es gibt dann, im Grunde genommen, nur eine einzige, aber mit 32 Springern!
Ein Schachbrett, dem zwei Ecken fehlen, mit Rechtecken pflastern: Bei einem normalen Schachbrett wurden zwei gegenüberliegende Eckquadrate entfernt und die Aufgabe gestellt, das restliche Brett mit bestimmten Rechtecken so zu belegen, dass kein Quadrat frei bleibt oder doppelt belegt wird. Jedes Rechteck bedeckt zwei kleine Quadrate des Schachbretts.


Schachbrett legen: Mit diesem Knobelspiel kannst Du das schöne Schachbrett vom Anfang des Artikels herstellen. Die Aufgabe besteht hier darin, aus den 14 Teilen ein Schachbrett zusammenzusetzen.


Wer mit dem vom Schachspiel her bekannten Rösselsprung (= Zug eines Springers) so seine Schwierigkeiten hat, der kann ihn mit folgender Aufgabe aus der Mathothek trainieren:

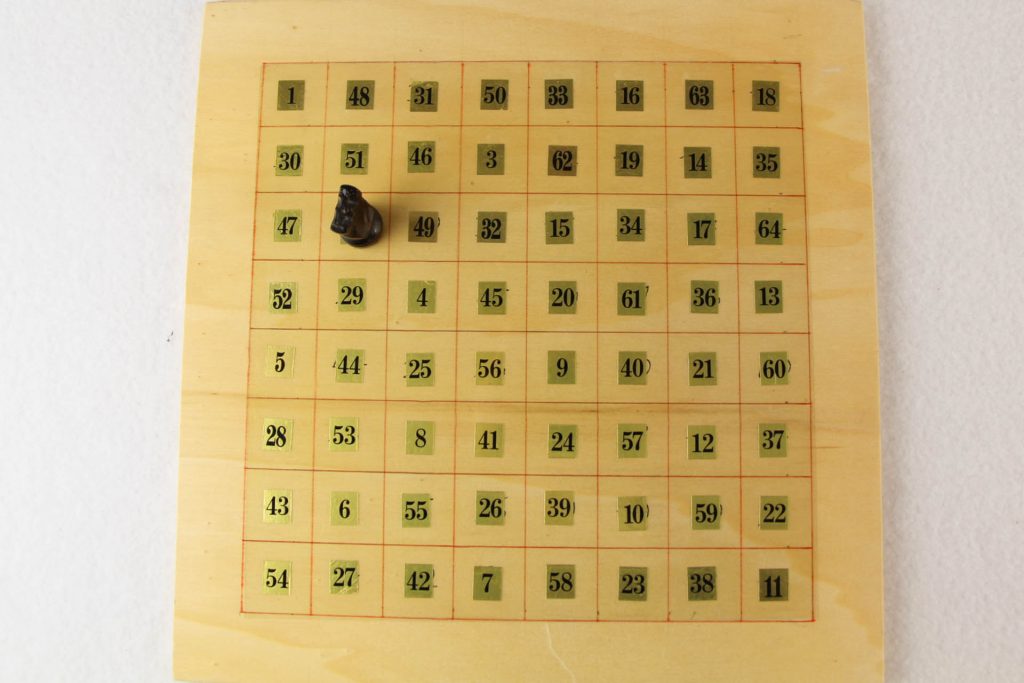
Springer und magisches Quadrat: Bei diesem Exponat der Mathothek sind ein 8×8-großes Zahlenquadrat und ein Springer mit seiner typischen Bewegung auf einem Schachbrett verknüpft: Die Zahlen von 1 bis 64 sind einerseits so verteilt, dass der schwarze Springer alle 64 Felder mit seiner typischen Zugform genau einmal betritt, andererseits so ein fast magisches Quadrat entsteht. Die Summen der Zahlen in jeder Zeile und auch in jeder Spalte sind immer gleich. Allerdings stimmen die Summen der beiden Diagonalen nicht überein, weshalb es sich hier um kein perfektes magisches Quadrat handelt.
Bei der Variante “Chex” hat sich bei dem “Beispiel für eine schnelle Bedrohung” ein Fehler eingeschlichen.
Schon nach dem zweiten Zug steht der weiße (!) König im Schach – durch den schwarzen Läufer auf dem braunen Feld.
Der weiße Läufer im dritten Bild hätte nicht so ziehen dürfen, er überspringt ja zwei andersfarbige Felder. Erlaubt wären nur die drei weißen Felder, die im Beispiel von Bauern besetzt sind (wenn sie frei wären), bzw. weitere Felder in den gleichen Richtungen
Echt ein toller Artikel.
Ideal um mit begabten Kindern weiterführende Strategie zu lernen