Wie können wir helfen?
Zum Einstieg sind hier vier Beispiele von Uhren mit Zeigern aus der Mathothek abgebildet. Darüber hinaus gibt es in der Mathothek eine stattliche Sammlung von Uhren, die jeweils interessante und meistens erstaunliche Besonderheiten aufweisen.
Von solchen “Zeiger-Uhren” kennen wir eigentlich schon alle seit Grundschultagen das “Kreis-Rechnen”. Deswegen habe ich mir eine weniger exotische Uhr ausgeliehen, die keine weiteren “mathothekischen” Besonderheiten besitzen:
Wie man sieht und ablesen kann, ist es im Moment der fotographischen Aufnahme 2:25 Uhr. Oder ist es 14:25 Uhr? Die Entscheidung ist dem Foto nicht zu entnehmen. Nach jeweils 12 Stunden zeigt die Uhr wieder die gleiche Zeigerstellung. Anhand weiterer Umstände müssen wir jeweils entscheiden, ob es 2:25 Uhr oder 14:52 Uhr ist. Beachten wir einmal nur den kleinen Zeiger, dann ergeben sich folgende Gleichheiten 0, 12, 24, 36, 48, … , aber auch 8, 20, 32, 44, 56, … und 5, 17, 29, 41, 53, … usw. Also wir benutzen eigentlich nur die Reste, die bei der Division durch 12 entstehen.
Ordnen wir die natürlichen Zahlen einmal bei der Division durch 5 in einem Kreis an, dann kann uns dabei folgendes Exponat der Mathothek helfen:
Auf dem innersten Kreis sind die fünf möglichen Reste bei der Division durch 5 fixiert. Die Aufgabe besteht nun darin, die Chips mit den Zahlen 0 bis 24 so auf die Kreise zu verteilen, dass auf jedem Radius die Zahlen den vorgegebenen Resten 0, 1, 2, 3 oder 4 liegen.
In der Mathematik ist “Kreisrechnen” natürlich Babysprache. Die Division mit Rest oder auch der euklidische Divisionsalgorithmus ist ein mathematischer Satz aus der Zahlentheorie und der Algebra. Dieser Satz besagt, dass es zu zwei Zahlen n und m, wobei m nicht 0 sein darf, eindeutig bestimmte Zahlen a und b so gibt, dass n=m⋅a+b gilt, wobei 0≤b und b<Betrag von m gültig ist. Der Rest ist also die Differenz zwischen dem Dividenden (der zu teilenden Zahl) und dem größten Vielfachen des Divisors (Teilers), das höchstens so groß ist wie der Dividend. Logisch, ein Rest (≠0) ergibt sich immer nur dann, wenn die zu teilende Zahl kein Vielfaches des Teilers ist, das heißt auch, dass der Dividend nicht durch den Divisor teilbar ist. Für dieses Experiment benötigt man nur die schon in der Grundschule gelernte schriftliche Division natürlicher Zahlen mit Rest.
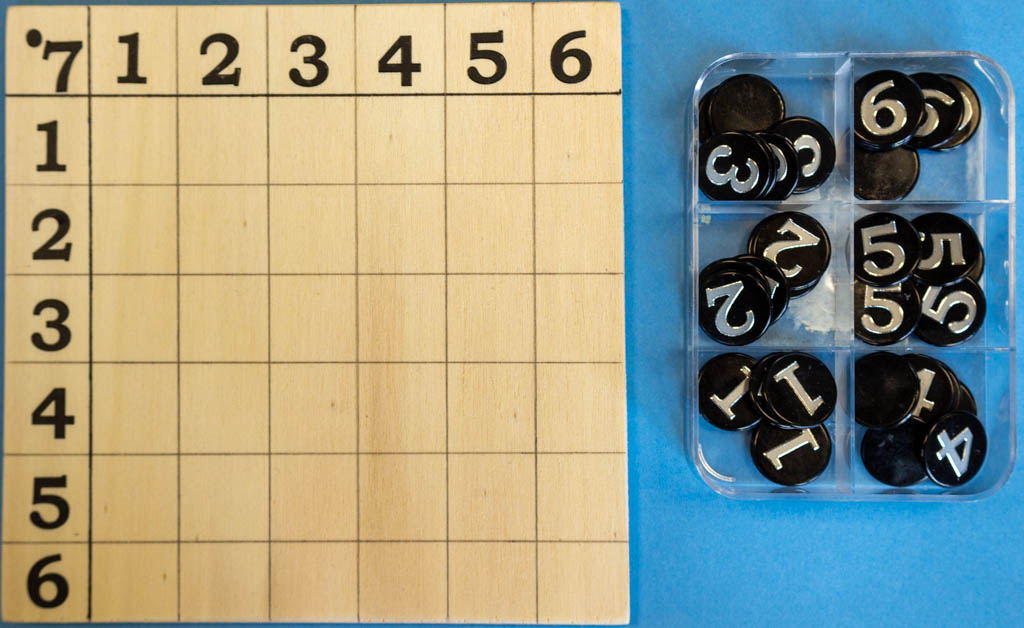
Zur Übung und Vertiefung gibt es ein weiteres Objekt in der Mathothek.
Es besteht aus einer Holzkiste mit sechs Fächern und hölzernen Chips mit natürlichen Zahlen, derselben Zahl auf beiden Seiten. Die Ziffern an den Seiten der Fächer 0, 1, 2, 3, 4 und 5 geben die möglichen Reste der blau unterlegten Zahlen bei der Division durch 6 an. Dazu lassen sich durchaus Spielideen entwickeln, um die Chips in die entsprechenden Fächer mit dem richtigen Rest bei der Division durch 6 zu verteilen.
Will man das Erkennen der Reste und damit das Einsortieren erleichtern, so sperrt man mit dem roten Chip das Fach für die Sechs und sortiert dann nach den Resten bei der Division durch 5. In diesem Fall ist nämlich die Teilbarkeit leichter festzustellen: Eine Zahl ist genau dann durch 5 teilbar, wenn ihre letzte Ziffer 0 oder 5 ist.
Hier das fertige Ergebnis:
Man bezeichnet diese Rechnung mit den Resten bei der Division mit einer festen Zahl (im Beispiel mit dem großen Zeiger der Uhr die 12) als Modulo-Rechnung: “42=6 (modulo 12)” oder “42 modulo 12=6”. Hier in der Mathothek möchte ich die Schreibweise “42=126″ (gesprochen: “42 ist kongruent 6 modulo 12” oder auch “42 ist 6 modulo 12”) verwenden. Dann ist gut verständlich, dass 42 und 6 sich nur durch ein Vielfaches von 12 unterscheiden, also 42=3⋅12+6 gilt, was klar und besser ist als die verbreitete Schreibweise 42:12=3Rest6.
Somit sind folgende Gleichungen leicht zu überprüfen: 17=52, 111=76 und 108=30. 17:5=3⋅5+2, also Rest 2, 111:7=16⋅7+6, also Rest 6 und 108=30, weil 108 durch 3 teilbar ist und damit der Rest 0 ist.
Wenn der Divisor festliegt, zum Beispiel die 7, dann spricht man auch von der Menge der Siebener-Reste {0, 1, 2, 3, 4, 5, 6}.
Nun kann man auch noch “im Kreis addieren” und manchmal auch “im Kreis multiplizieren”.
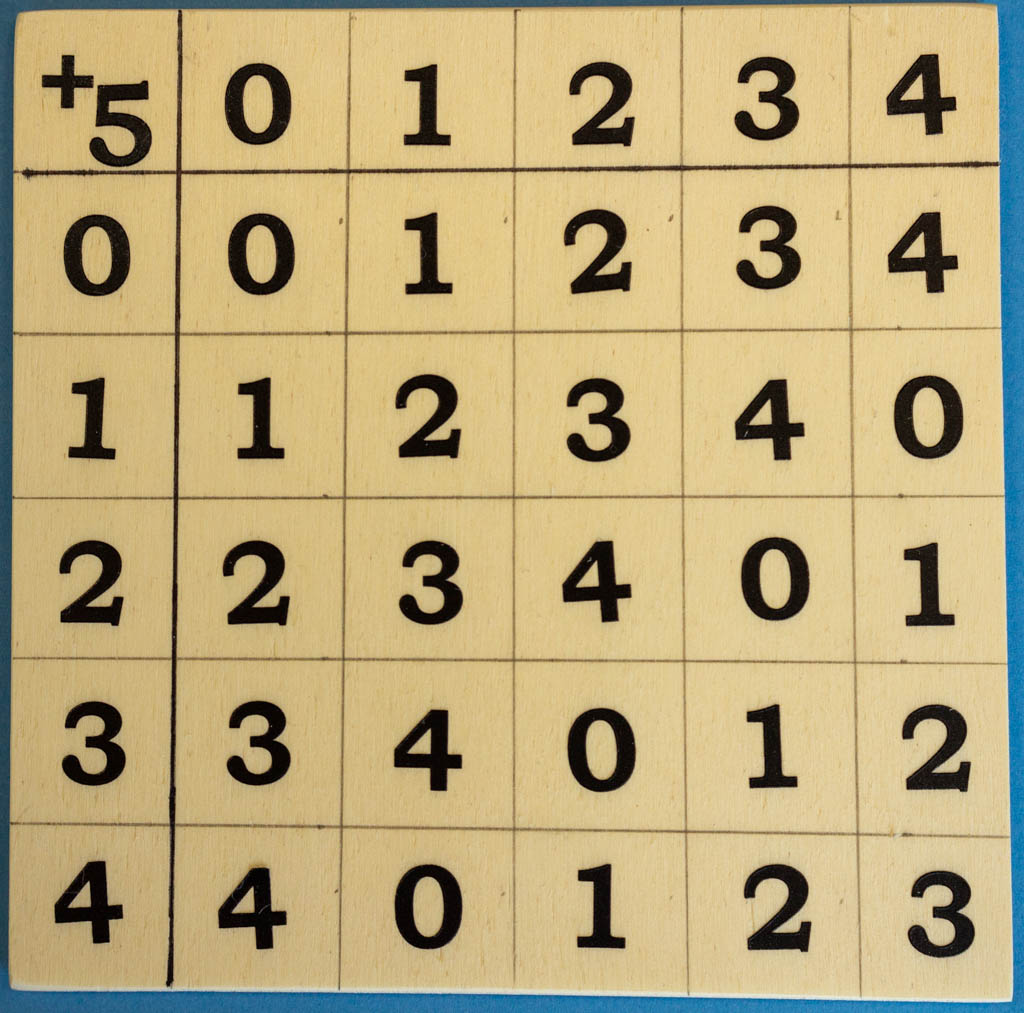
Als erstes Beispiel nehmen wir uns die Fünfer-Reste vor und betrachten die Additionstafel für das Modulo-Fünf-Rechnen:
Hierbei gibt es die möglichen Reste 0, 1, 2, 3 und 4. Die Summe (modulo 5) von 3 und 4 findet man im Schnittpunkt der 4. Zeile (Eingangszeile 3) und der 5. Spalte (Eingangsspalte 4): 3+54=2, (3+4=7=52). Das Ergebnis für 2+53 findet man in der waagrechten Eingangszeile 2 und in der Eingangsspalte 3. Es beträgt 0.
Auch für die Multiplikation (modulo 5) gibt es eine entsprechende Verknüpfungstafel:
Die Null taucht hier nicht auf. Es gilt jedoch auch hier 0⋅5x=0 für alle x. Und ganz wichtig: Ein Produkt ist nur dann 0, wenn wenigstens einer der Faktoren 0 ist.
Die Benutzungsregeln dieser Tafel sind dieselben wie bei der Verknüpfungstafel für die Addition modulo 5.
Das gilt auch für die Benutzung der Verknüpfungstafel für die Addition modulo 6:
Nachdem Du nun denkst, dass das natürlich genauso funktioniert wie eben, kommt eine bittere Überraschung:
Es tauchen beim ⋅6Rechnen plötzlich vier Nullen auf, obwohl von den beiden Faktoren keiner 0 ist: 2⋅63=0, 3⋅62=0, 3⋅64=0 und 4⋅63=0. Tatsächlich sind 2⋅3 und 3⋅4 durch 6 teilbar, ergeben also den Rest 0.
Aber es geht auch hier mit rechten Dingen zu: Wie man sieht, liegt der Grund darin, dass 5 eine Primzahl ist und 6 nicht!
Um Dein Vertrauen zu stärken, bekommst Du in der Mathothek noch ein weiteres interaktives Objekt angeboten:
Und nun die Lösung der “lebenswichtigen” Frage nach dem Wochentag in 4217 Tagen:
Und hier die Antwort:
Modulo, also der ganzzahlige Rest beim euklidischen Divisionsalgorithmus, wird für zahlreiche Verschlüsselungsverfahren und auch für Schlüsselaustausch-Verfahren benötigt.