Wie können wir helfen?
Bei diesem Exponat der Mathothek handelt es sich um ein Kästchen mit zwei recht langen Ketten aus bunten Holzperlen. Genaueres Betrachten liefert die Erkenntnis, dass es sich bei beiden Kostbarkeiten um gleichgroße Perlen in zehn verschiedenen Farben handelt. Soweit reicht die Übereinstimmung.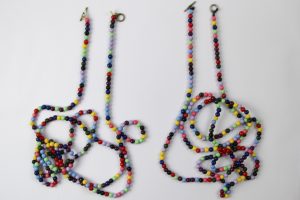 Gibt es einen wesentlichen Unterschied bei diesen beiden so ähnlichen “Mustern”? Entscheiden Regeln über die Verteilung der Farben oder herrscht der pure Zufall?
Gibt es einen wesentlichen Unterschied bei diesen beiden so ähnlichen “Mustern”? Entscheiden Regeln über die Verteilung der Farben oder herrscht der pure Zufall?
Auf den ersten Blick sehen die beiden Ketten zwar sehr ähnlich aus und es riecht ganz nach reinem Zufall, denn es fallen hinsichtlich des Verteilungsmusters keine markanten Unterschiede auf. Jeder Besucher wird aber zwangsläufig nach einem Muster oder einem Prinzip suchen, weil wir Menschen ungern mit Zufall und Chaos konfrontiert werden und auch hier einen tieferen Sinn sehen wollen. In diesem Fall wird der Suchende vermutlich aber wegen Erfolglosigkeit früher oder später aufgeben. Doch kann dem Strebenden auch hier geholfen werden. Tatsächlich gibt es eine höchst überraschende Erklärung:
Jede Perlenfarbe entspricht einer Zahl zwischen 0 und 9, und zwar ist diese Zuordnung bei beiden Ketten gleich. Bei der einen Kette erfolgte die Auswahl und Reihenfolge der aufgefädelten Perlen mit einem Zufallsgerät. Die Farbgebung der Kette erfolgte in dem Fall völlig zufällig.
Bei der zweiten Kette wurde die Auswahl der Perlen bezüglich ihrer Farben so getroffen, dass ihre Reihenfolge den Ziffern der Zahl Pi (π=3,141592653…) entspricht.
Wenn man weiß, dass eine der beiden Ketten der Ziffernfolge der Zahl π entspricht, so kann man sie als die rechte identifizieren. Nur bei dieser Kette gibt es eine Farbverteilung, die dem Anfang der Zahl π in der Dezimaldarstellung entspricht.
So zeigt dieses Exponat, dass uns etwas völlig zufällig und chaotisch erscheinen, sich dahinter aber eine tief liegende mathematische Gesetzmäßigkeit verbergen kann.
Es gibt bezüglich der Eigenschaften der Zahl eine ganze Reihe, die seit mehr oder weniger langer Zeit bewiesen sind. Bis heute ist aber die Frage, ob π normal ist, weder bewiesen noch widerlegt worden. Dabei bedeutet “normal” ziemlich genau das, was wir aus dem Vergleich der beiden Ketten am Anfang vermuteten, dass die Ziffernfolge von π als “Zufallsgenerator” benutzt werden kann. Eine reelle Zahl ist normal, wenn in ihrer Ziffernfolge
- Ziffernblöcke jeder Länge vorkommen und
- alle Ziffernblöcke, die dieselbe Länge haben, auch noch mit derselben relativen Häufigkeit auftreten.


