Wie können wir helfen?
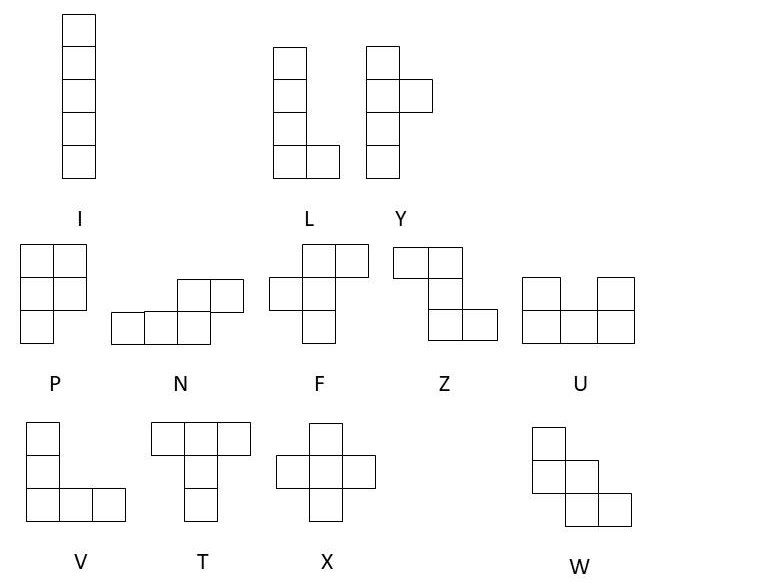
Ein Pentomino oder auch Pentamino ist eine geometrische Figur, die aus fünf kongruenten Quadraten zusammengesetzt ist, wobei die Quadrate an Kanten zusammenhängen. Insgesamt gibt es, wenn man von Symmetrien (Spiegelungen und Drehungen) absieht, zwölf Typen. In einer gewissen Analogie zu unseren Buchstaben ergibt sich folgende Übersicht:
Die orientierten (=nicht achsensymmetrischen) Pentominos L, Y, P, N, F und Z stimmen nicht mit ihren Spiegelbildern überein. Jedoch kann man sie als weitere Möglichkeiten benutzen, indem man sie wendet. Auf diese Weise erhält man bei den Legespielen insgesamt 12+6=18 Möglichkeiten.
Mit jedem der zwölf Pentominos lässt sich die Ebene parkettieren, d.h. man kann mit jeder Pentominoform die gesamte Ebene so ausfüllen, dass weder eine Überlappung noch eine Lücke entsteht. Bei den orientierten Pentominos geht das sogar ohne ihre Spiegelbilder.
Alle Pentominos lassen sich aus den Ausgangspentominos zusammensetzen, d.h. selbstähnlich vergrößern.
Es gibt verschiedene Aufgabenstellungen, z.B. soll man mit allen 12 Pentominos Rechtecke mit den Seiten 6mal10, 5mal12, 4mal15 und 3mal20 bilden.
Eine andere Aufgabenstellung besteht darin, mit allen zwölf Pentominos und einem 2×2-Quadrat ein vorgegebenes Quadrat zu legen.
Bei der nächsten Aufgabenstellung stehen nur 11 der 12 Pentominos zur Verfügung. Damit die quadratische Form 8×8 vollständig gefüllt werden kann, gibt es noch vier Polyominos, die aus einem, zwei oder vier Würfeln bestehen.
Dazu gibt es in der Mathothek mehrere Legespiele, z.B. mit einem Quadrat aus 36 kleinen kongruenten Quadraten. Die Aufgabe lautet hier, mit den sieben gegebenen Pentominos das große Quadrat so zu belegen, dass nur eine Zahl des inneren Quadrates freibleibt. Natürlich sollte man diese Zahl vor Beginn festlegen. Legt man das große Quadrat mit den erlaubten sieben Pentominos vorschriftsmäßig aus, so werden immer 7⋅5=35 kleine Quadrate belegt und eine Zahl bleibt frei.
Ein zweites ähnliches Legespiel stammt aus dem Shop des Gießener Mathematikums. Es enthält 31 kleine Quadrate und ein 1mal4 großes Rechteck, die ein 5mal7 großes Rechteck ausfüllen. Zum Belegen des gesamten Rechtecks stehen dann sieben der möglichen zwölf Pentominos zur Verfügung. Man kann aber auch, wenn man es mit sechs der sieben Pentaminos entsprechend der Anleitung auslegt, als einzige Zahl seinen Geburtstag sichtbar lassen und das Rechteck mit dem Text Pentomino-Kalender
Diese Aufgabe ist ebenso wie die erste Aufgabe immer lösbar, wenn auch nicht immer auf Anhieb. Alle 31 Lösungen sind deshalb am Ende dieses Artikels zu sehen.
Man kann aber nicht nur fünf kongruente Quadrate zu solchen geometrischen Figuren in der Ebene an den Kanten zusammenfügen, sondern jede Zahl, in dem Fall spricht man von Polyominos. Natürlich ist das für zwei geometrisch ziemlich uninteressant, da es nur eine Möglichkeit gibt, zwei kongruente Quadrate an jeweils einer Kante aneinander zu fügen. Nur beim Dominospiel spielen solche “Duominos” eine wesentliche Rolle. Aber es lassen sich auch interessante Aufgabenstellungen für Dominosteine finden, beispielsweise gibt es in der Mathothek ein Schachbrett mit zwei entfernten Eckquadraten und die Aufgabenstellung, die restlichen Felder des Schachbretts mit Dominosteinen so zu belegen, dass Felder weder doppelt besetzt werden noch freibleiben.
Auch mit “Triominos”, für die es nur zwei Möglichkeiten gibt, ist es nicht besonders interessant. Aber mit Quadrominos, die aus vier gleichen Quadraten zusammengesetzt sind, werden Legespiele recht interessant. Dabei gibt es fünf Quadrominos, wie man leicht herausfindet.
Bei den nächsten Legespielen geht es um Quadrominos. Wie man dabei sieht, stehen die fünf Quadrominos mehrfach zur Verfügung. Die untere und die obere Seite der Quadrominos sind hell bzw. dunkel gefärbt.
Auch bei diesen Quadrominos geht es darum, das Quadrat auszufüllen. Allerdings handelt es sich nur um eine Restfläche dieses Quadrates. In den Ecken und in den Mitten am Rand jeder Seite sind mit Quadraten Lücken für die Belegung vorgesehen.
Dieses Spiel enthält 14 Quadrominos, die zwei unterschiedliche Seiten haben. Die Vorderseiten sind hell oder dunkel lackiert, die Rückseiten sind schwarz. Es dürfen nur die hellen und dunklen Vorderseiten nach oben gelegt werden. Grundsätzlich sollen alle Quadrominos in den quadratischen Rahmen gelegt werden. Dabei sind einige quadratische Bereiche ausgespart worden. Dazu gibt es verschiedene Schwierigkeitsstufen:
- Alle 14 Quadrominos sollen in das quadratische Feld gelegt werden. Dabei bleiben fünf beliebige Felder frei
- Beim Hineinlegen der 14 Quadrominos sollen mithilfe der fünf Freiflächen eins der zwölf Pentominos gebildet werden (es gibt also zwölf Möglichkeiten)
- Die 14 Teile sollen so in dem Rahmen verteilt werden, dass mithilfe der beiden unterschiedlichen Farben je zwei zusammenhängende Flächen mit fünf zusammenhängenden Freiflächen dazwischen entstehen. Die Freiflächen sollen eines der Pentaminos bilden (es gibt also auch hier zwölf Möglichkeiten)
Hier sind die richtigen Lösungen für die zweite Aufgabe:
Das sind die richtigen Lösungen für die zweite Aufgabe:
Besonders viele Möglichkeiten, geometrische Formen zu legen, ergeben sich mit Hexominos oder Hexaminos. Allerdings gibt es in der Mathothek Hexaminos nur, die aus gleichseitigen Dreiecken zusammengesetzt sind. Dabei gibt es – wieder ohne Drehungen und Spiegelungen – zwölf Grundfiguren. Als Anregung und Hilfe gibt es eine Anzahl Vorlagen.
Ziemlich knifflig sind zwei Legespiele aus solchen Hexaminos mit vorgegebenen Rahmen. Bei dieser hexagonalen Form wird die Lösung noch erschwert dadurch, dass man die Spiegelbilder der neun Hexaminos nicht verwenden darf.
Bei dieser Aufgabe werden alle zwölf Hexaminos benötigt, um die sternartige Form zu füllen.
Es gibt auch Polyominos in der Mathothek, die nicht aus Quadraten zusammengesetzt sind, sondern analog aus regelmäßigen Sechsecken. Hier ist ein solches Legespiel aus den elf möglichen Kombinationen aus Hexagonen, aus denen sich mit Kreativität verschiedene Formen zusammensetzen lassen.
Stellt sich nun noch die Frage: Gibt es außer Quadraten, gleichseitigen Dreiecken und regulären Sechsecken noch andere reguläre Vielecke, aus denen sich Polyominos machen lassen? Nein! Nur mit diesen drei regulären Vielecken kann man die Ebene parkettieren:
Und hier die Lösungen für das Kalenderproblem:
Und hier die Lösungen für die quadratischen Pentomino-Probleme:
Die Lösung für das vierte Pentominospiel unterscheidet sich von den anderen, weil es nur elf Pentominos gibt und darüber hinaus vier Bausteine, die keine Pentominos sind.