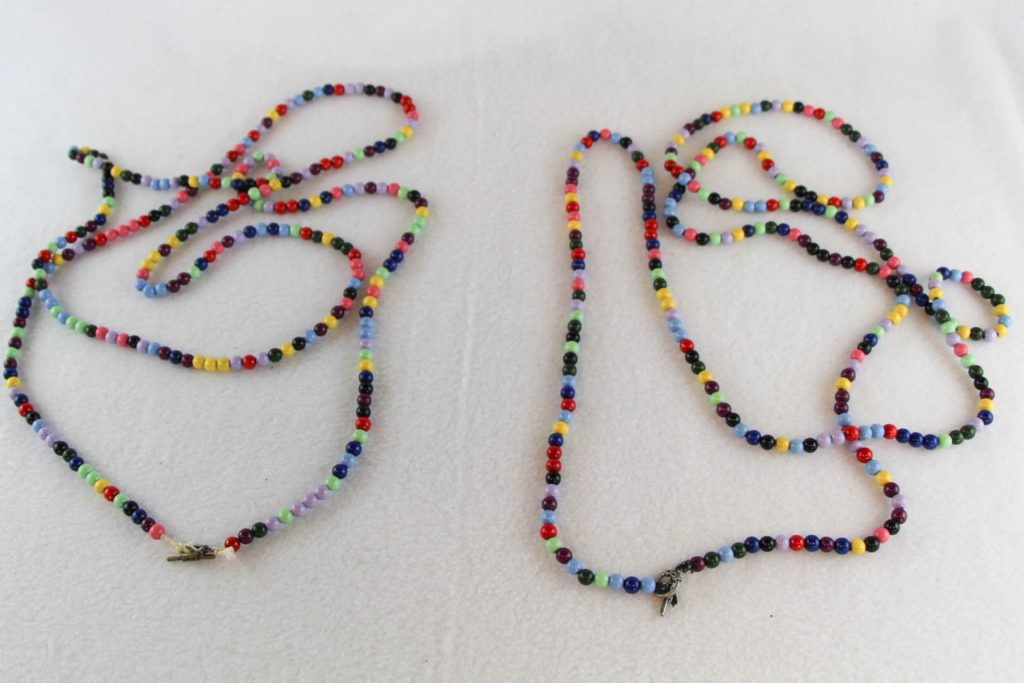Wie können wir helfen?
Die Assoziation von der Folge der natürlichen Zahlen: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, … und auf einem Faden aufgereihten Perlen ist nicht wirklich überraschend. So läge es nahe, bestimmte Eigenschaften dieser nicht nur für die Mathematik so grundlegenden Elemente in Form von Modeschmuck zu nutzen und sichtbar zu machen. Während bei den verbreiteten Modeschmuckketten die Anordnungen der Perlen meistens schnell durchschaut werden kann und weitgehend von symmetrischen Gesichtspunkten bestimmt werden, fordert diese Art von “mathematischem Schmuck” gerade durch seine Asymmetrie dazu heraus, nach verborgenen Mustern zu suchen. Sie zu entdecken, bedeutet dann, wesentliche mathematische Eigenschaften der Zahlen zu erkennen. So einfache Beziehungen wie das Gerade- oder Ungeradesein oder die Teilbarkeit durch eine bestimmte Zahl kommen im Modeschmuck häufig vor und sind deshalb unter den Objekten der Mathothek nicht vertreten.
Bei der Permutationskette geht es um die möglichen Anordnungen von vier verschieden farbigen Holzperlen. Jede der möglichen Permutationen ist von der nächsten durch eine kleine schwarze Perle getrennt. Wie man sehen kann, gibt es für die vier Perlen insgesamt 24 mögliche verschiedene Anordnungsmöglichkeiten. Das erklärt sich so: Die erste Perle wähle ich aus vier vorhandenen Perlen aus, das sind also vier Möglichkeiten, für die Auswahl der zweiten habe ich nur noch drei Möglichkeiten, für die Auswahl der zweiten nur noch zwei und für die letzte gibt es natürlich nur noch eine. Insgesamt ergeben sich somit 4 · 3 · 2 · 1, das ergibt die 24 vorhandenen Permutationen.
Für das Produkt n · (n – 1) · (n – 2) … 2 · 1 sagt man “n-Fakultät” und schreibt n!.
____________________________________________________________
Bei der Vielfachenkette stehen die Perlen für die Zahlen 1, 2, 3, bis 96. Jeder durch sechs teilbaren Zahl entspricht eine gelbe oder grüne Perle, die gelben bzw. grünen Perlen sind also Vielfache von sechs. Die blauen und grünen Perlen entsprechen den Zahlen, die Vielfache von acht sind. Zahlen, die sowohl Vielfache von sechs als auch von acht sind, entsprechen somit den grünen Perlen “gemeinsame Vielfache von sechs und acht “. Das “kleinste gemeinsame Vielfache von sechs und acht” ist also 24 und entspricht der ersten grünen Perle.
____________________________________________________________
Bei der Primzahlenkette III sind die ersten Primzahlen 2, 3, 5, 7, 11, 13, 17, 19 und 23 jeweils mit entsprechend vielen Holzperlen einer Farbe dargestellt. Dasselbe gilt für die Primzahlenkette I.
Primzahlen sind die “Atome der natürlichen Zahlen”. Eine Primzahl hat genau zwei Teiler. Jede Primzahl lässt sich nur durch eins und sich selber teilen, wobei die Eins keine Primzahl ist. Das hat mit dem “atomaren Charakter” der Primzahlen zu tun: Jede natürliche Zahl kann so eindeutig als Produkt von Primzahlen geschrieben werden. 24 = 2· 2 · 2 · 3, 30 = 2 · 3 · 5 und 70 = 2 · 5 · 7 sind drei Beispiele dafür.
____________________________________________________________
Bei der Primzahlenkette I entsprechen die Holzperlen der Folge der natürlichen Zahlen. Dabei sind die Zahlen, die den blauen Perlen entsprechen, Primzahlen. Die orangefarbenen Perlen dagegen entsprechen den Nicht-Primzahlen. Diese Kette ließe sich unendlich fortsetzen, ohne dass irgendwann nur noch orangefarbene Perlen aufträten. Das wissen wir schon mehr als 2000 Jahre lang. Schon der große antike Mathematiker Euklid hat nämlich bewiesen, dass es keine größte Primzahl geben kann.
____________________________________________________________
Bei der Fibonacci-Kette II werden die natürlichen Zahlen 1, 2, 3, 4 und 5 als Summen von Einsen und Zweien – runde bzw. längliche Holzperlen – dargestellt. So ergeben sich für die Zahl vier folgende Möglichkeiten: 1 + 1 + 1 + 1, 1 + 1 + 2, 1 + 2 +1 , 2 + 1 + 1 und 2 + 2, also fünf Möglichkeiten. Die Anzahl der Möglichkeiten sind die ersten Fibonacci-Zahlen.
____________________________________________________________
Schon die alten Griechen hatten großen Spaß daran, besonders interessante Eigenschaften bei den Zahlen herauszufinden. So entdeckten sie die “Vollkommenheit” mancher Zahlen. Die kleinste vollkommene Zahl ist schnell gefunden: Es ist die Zahl sechs. Addiert man alle echten Teiler von 6, das sind 1, 2 und 3, so erhält man 1 + 2 + 3 = 6. Eine vollkommene Zahl ist daran erkennbar, dass die Summe ihrer Teiler – ohne die Zahl selbst – die Zahl selbst ist. Bei dem vollkommenen Ring, Armband und der vollkommenen Kette in der Mathothek geht es um die ersten drei vollkommenen Zahlen: 6, 28 und 248. (28 = 1 + 2 + 4 + 7 + 14 und 248= 1 + 2 + 4 + 8 + 31 + 62 + 124)
____________________________________________________________
Bei befreundeten Zahlen besteht obige Eigenschaft zwischen zwei verschiedenen Zahlen, d.h. die Teiler der ersten Zahl ergeben addiert die zweite Zahl und die Summe der Teiler der zweiten Zahl entspricht der ersten Zahl. Bei den beiden Freundschaftsketten handelt es sich um das kleinste befreundete Zahlenpaar, nämlich 220 und 284. Die echten Teiler von 220 bilden die Summe 1 + 2 + 4 + 5 + 10 + 11 + 20 + 22 + 44 + 55 + 110 = 284 und die echten Teiler von 284 bilden die Summe 1 + 2 + 4 + 71 + 142 = 220.
____________________________________________________________
Bei der Binärkette werden die Zahlen von eins bis fünfzehn als Binärzahlen dargestellt. Eine schwarze Perle steht für eins, eine weiße für null und die kleineren rötlichen Perlen dienen zur Trennung. Das Zweiersystem braucht nur die Ziffern 0 und 1, um jede Zahl darzustellen. Diese Möglichkeit ist zwar schon lange bekannt, erfuhr aber seine grundlegende Anwendung erst mit dem Computer im digitalen Zeitalter.
____________________________________________________________
Bei der Quadratzahlen-Kette stehen die Perlen wieder für die natürlichen Zahlen und die “goldenen Perlen” entsprechen den Quadratzahlen: 1, 4, 9, 16 bis 100.
____________________________________________________________
Bei der ggT-Kette geht es um den größten gemeinsamen Teiler zweier Zahlen. Die Zahlen sind hier durch die entsprechenden Anzahlen von Holzperlen dargestellt. der größte gemeinsame Teiler zweier benachbarter Zahlen stimmt mit der Anzahl der dunklen Perlen überein. Es handelt sich hier um die Zahlen 36, 24, 40 und 9 und entsprechend um ggT(36,24) = 12, ggT(24,40) = 8 , ggT(40,9) = 1 und ggT(9,36) = 9. Die Zahlen 40 und 9 haben nur die Eins als gemeinsamen Teiler. Solche Zahlen nennt man “relativ prim” zueinander.
____________________________________________________________
Bleiben zum Schluss nur noch die kleinen Armbändchen. Jedes der 32 Armbänder enthält eine mögliche Teilmenge von fünf verschieden farbigen Perlen, dabei gibt es auch ein Bändchen ohne Perlen und eines mit allen fünf Perlen, denn auch die leere Menge und die Grundmenge zählen zu den Teilmengen. Auf diese Weise gibt es zu jeder Menge von n Elementen genau 2n Teilmengen. Die Menge aller Teilmengen einer bestimmten Menge nennt man auch die Potenzmenge dieser Menge. Sie spielt in der Mengenlehre des Mathematikers Cantor eine sehr wichtige Rolle bei der Untersuchung und Unterscheidung unendlicher Mengen.
Ähnliche Objekte
→