Wie können wir helfen?

Bei manchen Brettspielen nervt es, wenn man mehrere Runden mit dem Einsatz warten muss, weil man keine Sechs würfelt. Aber es ist auch gar nicht so selten, dass man dann anschließend noch eine Sechs wirft. Natürlich spielt hier auch unsere Psyche eine Rolle: Eine solche Glückssträhne bleibt besonders im Gedächtnis hängen.

Es gibt 36 mögliche Ausgänge für zweimaliges Werfen eines normalen Würfels: (1/1), (1/2), (1/3), (1/4), (1/5), (1/6), … (6/1), (6/2), (6/3), (6/4), (6/5), (6/6), sodass die Wahrscheinlichkeit für “zweimal eine Sechs hintereinander”= {(6/6)} nur 1/36 beträgt.
Wie groß ist die Wahrscheinlichkeit dafür, dass man überhaupt zufällig zweimal dieselbe Zahl erhält? Das dazugehörige Ereignis A={(1/1), (2/2), (3/3), (4/4), (5/5), (6/6)}=”Pasch” hat dann die Wahrscheinlichkeit 6/36=1/6.

Wir betrachten nun einige Beispiele für Experimente zu “mindestens zweimal das Gleiche”:
Beispiel 1: Wir benutzen dazu vier gleichfarbige normale Würfel und werfen diese gleichzeitig. Wie groß ist die Wahrscheinlichkeit, dass eine Augenzahl mehr als einmal vorhanden ist? Hier sind die Ergebnisse von sechs Würfen mit vier grünen Würfeln:
Nur beim ersten und beim letzten Wurf sind alle Ergebnisse verschieden. Die anderen gehören alle zum Ereignis “Mindestens zweimal das Gleiche“, d.h. das Verhältnis für Ausfälle “mit mindestens eine Augenzahl kommt mehrfach vor” (Ereignisse) zu allen Ausfällen steht 4:6.
Insgesamt sind 64=1296 Ausfälle möglich. Ergebnisse, bei denen nur verschiedene Augenzahlen auftreten, gibt es 6⋅5⋅4⋅3=360. Somit erhalten wir die Gleichung 1-360/1296=0,7222…, d.h. mit einer Wahrscheinlichkeit von ca. 72 % erhalten wir mindestens eine Augenzahl, die mehr als einmal erscheint. Was durchaus zu unserem oben dokumentierten Experiment passt (4/6= 0,666…).
Beispiel 2: Wir nehmen diesmal je zwei rote und grüne Würfel. Gleiches Ergebnis bedeutet jetzt, dass beide Würfel dieselbe Farbe haben und dieselbe Augenzahl zeigen. Hier die Ergebnisse der ersten 9 Würfe:
Es gibt nun 6⋅5 Möglichkeiten, mit den beiden roten Würfeln nur verschiedene Augen zahlen zu würfeln, ebenso sind es insgesamt 6⋅5 Möglichkeiten für die beiden grünen Würfel. Insgesamt gibt es dann (6⋅5)⋅(6⋅5) mögliche Ausfälle mit nur verschiedenen Würfeln zu bekommen. Alle Möglichkeiten zusammen sind in unserem Fall 6⋅6⋅6⋅6=64. Daher beträgt die Wahrscheinlichkeit mit den beiden roten und den beiden grünen Würfeln “mindestens zweimal das Gleiche” zu erhalten: 1-62⋅52/64≈69 %.
Bei unserem kleinen Experiment mit sechs Würfen waren wir viermal erfolgreich, also in ungefähr 67 % der Fälle.
Beispiel 3: Wir verwenden nun sechs gleiche Ikosaeder-Würfel mit den Zahlen von 1 bis 20 und würfeln damit viermal. Die Ergebnisse sind unten abgebildet.
Nur beim zweiten Wurf sind alle Augenzahlen verschieden. In den anderen drei Ergebnissen ist jeweils mindestens eine Augenzahl mehrfach vorhanden. Theoretisch gibt es bei sechs Ikosaeder-Würfeln 206=64000000 mögliche Ergebnisse, davon sind 20⋅19⋅18⋅17⋅16⋅15=27907200 Ergebnisse, bei denen alle Augen Zahlen verschieden sind. Folglich ergibt sich die Wahrscheinlichkeit für “Mindestens zweimal das Gleiche”=1-0,43605=0,56395, d.h. ca. 56 %.
Beispiel 4: Diesmal benutzen wir je drei rote, blaue und weiße Oktaeder-Würfel mit den Zahlen von eins bis acht. Bei den ersten vier Würfen traten folgende Ergebnisse auf:
“Gleich” heißt hier, dass sowohl die Augenzahl als auch die Farbe dieselben sein müssen. Somit tritt beim ersten Wurf zweimal die blaue Fünf auf, beim zweiten zweimal die rote Sechs, beim dritten Wurf erscheinen nur verschiedene Ergebnisse und beim vierten Wurf zweimal die weiße Fünf und zweimal die blaue Drei. Also sind bei drei von den vier Beispielen “mindestens zweimal das Gleiche” und nur einmal “alle verschieden”.
Wahrscheinlichkeitstheoretisch ergeben sich hier insgesamt 89 mögliche Ergebnisse und 8⋅7⋅6 mögliche Ergebnisse auf bei denen keine gleichen Augenzahlen bei den roten Würfeln auftritt, ebenso viele Möglichkeiten gibt es bei den drei blauen und den drei weißen Würfeln. Somit ergeben sich zusammen (8⋅7⋅6)3 Ergebnisse, bei denen keine gleichen Augenzahlen mit derselben Farbe auftreten. Die gesuchte Wahrscheinlichkeit für “zweimal das Gleiche” beträgt also 1-(8⋅7⋅6)3/89≈72 %, sodass das Experiment im Nachhinein nicht überraschend erscheint.
Das Geburtstagsparadoxon
Nimm einmal an, Du kommst in eine neue Klasse und erkundigst Dich, wer am gleichen Tag wie Du Geburtstag hat. Nimm weiter an, dass in der neuen Klasse 32 Kinder (mit Dir) sind. Wie groß ist die Wahrscheinlichkeit, dass noch mindestens ein Kind am selben Tag wie Du Geburtstag hat?
Wie oben rechnen wir die Gegenwahrscheinlichkeit, also die Wahrscheinlichkeit, dass niemand der anderen 31 Kinder an Deinem Geburtstag auch geboren wurde: 365 Tage stehen zur Verfügung, einer ist Dein Geburtstag, bleiben noch 364 Tage für die anderen. Somit erhalten wir als Wahrscheinlichkeit 36431:36531= (364/365)31≈0,918 und somit die beträgt die gesuchte Wahrscheinlichkeit dafür, dass noch wenigstens eines der anderen Kinder mit Dir am selben Tag Geburtstag hat, etwa 9 %.
Etwas anders sieht die Sache allerdings aus, wenn Du Dich fragst, wie wahrscheinlich es ist, dass überhaupt zwei oder mehr Kinder am selben Tag Geburtstag haben. Hier ergibt die Rechnung eine Wahrscheinlichkeit von 75 %. Dieses Ergebnis ist erstaunlich hoch. Aber die beiden Ausgangsfragen sind auch sehr verschieden.
Unten sind die konkreten Geburtstagsdaten von fünf Klassen abgebildet, die in der Mathothek zur Verfügung stehen. Diese realen Daten zufällig ausgewählter Klassen entsprechen durchaus der theoretischen Erwartung.
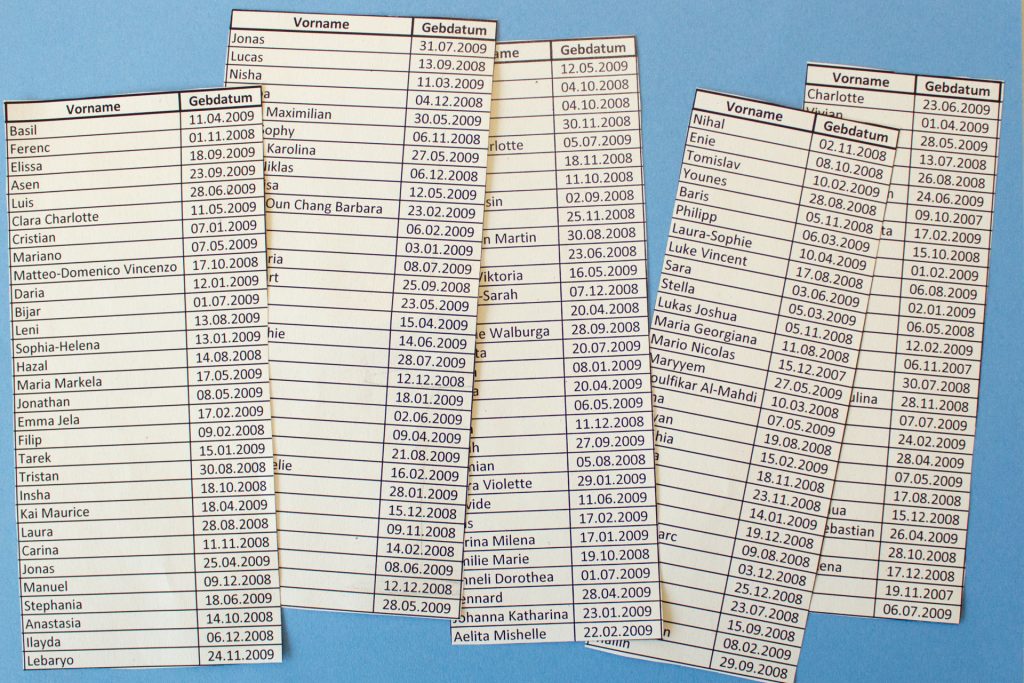
So bleibt am Ende nur noch die Frage, ab welcher Anzahl von Personen man daraufsetzen sollte, dass mindestens zwei davon am selben Tag Geburtstag haben. Die Antwort lautet: “Ab 23 Personen beträgt die Wahrscheinlichkeit über 50 %!”



















