Wie können wir helfen?
Das kleinste magische Quadrat ist auch wohl das älteste, nämlich das Lo Shu. Nach einer chinesischen Legende soll eine Schildkröte vor über 4000 Jahren aus einem Fluss gestiegen sein, die dieses magische Quadrat auf den Platten ihres Rückenpanzers getragen habe. Mit den geheimen Zauberkräften dieses kleinsten aller magischen Quadrate konnten die Menschen den Fluss dann in der Zukunft beherrschen.

Leider sind die Zeichen inzwischen etwas zerlaufen, aber sie sind immer noch als Zeichen für die Zahlen 1, 2, 3, 4, 5, 6, 7, 8 und 9 zu erkennen. In der obersten Zeile erkennt man 2, 7, 6, in der mittleren Zeile 9, 5, 1 und in der untersten 4, 3, 8. Addiert man diese drei Zahlen, so erhält man jeweils die Summe 15. Addiert man die Zahlen 2, 9, 4 der ersten (linken) Spalte, so ergibt das ebenfalls die Summe 15, die man auch erhält, wenn man die Zahlen 7, 5, 3 der zweiten Spalte und die Zahlen 6, 1, 8 der dritten Spalte addiert. Aber auch die Summen der Zahlen der beiden Diagonalen, 4, 5, 6 und 2, 5, 8 ergeben jedes Mal 15.
Mit einem kleinen interaktiven Objekt in der Mathothek kann jeder Besucher selbst magische Quadrate der Ordnung 3 finden. Eine große Hilfe ist die Kenntnis der magischen Konstanten, die sich hier ergibt durch folgende Rechnung (1+2+3+4+5+6+7+8+9):3=15. Weiterhin überlegt man sich leicht, dass die Fünf in der Mitte des 3×3-Quadrats ihren Platz haben muss.


Später in römischer Zeit bekam dieses kleinste magische Quadrat den Namen “Saturnsiegel”. Jedem der Planeten und auch Sonne und Mond hatte man ein besonderes magisches Quadrat zugeordnet und die den Himmelskörpern zugesprochenen Eigenschaften auch auf ihre zugeordneten magischen Quadrate übertragen.
Ein schon wohl vor dem Christentum entstandenes “magisches Quadrat mit Buchstaben”, auch SATOR-Quadrat genannt, diente auch später in christlicher Zeit noch umgedeutet als Glück bringendes Amulett.
Zwar gibt es hier weder Zahlen noch eine magische Konstante, aber eine Fülle interessanter Symmetrien. Zeilen und Spalten können vor- und rückwärts gelesen werden: SATOR↔ROTAS, AREPO↔OPERA und TENET↔TENET:

Das symmetrische Wort TENET bildet ein griechisches Kreuz. In den vier entstehenden Eckquadraten und in den Diagonalen sind weitere symmetrische und fast-symmetrische Beziehungen zu entdecken.
Aber was bedeutet nun der geheimnisvolle Text? Nicht alle sind sich hier einig. Es handelt sich wohl um lateinische Bezeichnungen mit der Bedeutung “Der Sämann Arepo sorgt mit seinen Händen dafür, dass sich die Räder drehen.” Auch über die Frage, ob Arepo tatsächlich ein Eigenname ist, gibt es Diskussionen. Später haben die Christen dieses magische Amulett übernommen und in ihrem Sinne umgedeutet. Sator (Sämann) stand bei ihnen nicht nur in diesem magischen Text für Gott, den Schöpfer der Welt.
Sicher ist, dass die Menschen in der symmetrischen Form und dem geheimnisvollen Text magische Kräfte vermuteten.
Johann Wolfgang von Goethe beschreibt in seinem Werk Faust Teil I ein Gemurmel der Hexe, in dem Zahlen und Rechnungen vorkommen. Möglicherweise enthält dieses dunkle Hexeneinmaleins die Beschreibung eines fastmagischen Quadrats, das sich aus dem Saturnsiegel ergibt. In der Mathothek gibt es ein interaktives Exponat und ein hübsches Büchlein zu dieser Stelle im Faust. Hier zunächst den Text des Hexeneinmaleins:
Du musst versteh’n! / Aus Eins mach Zehn, / Und Zwei lass geh’n, / Die Drei mach gleich, / So bist Du reich.
Man kennt jetzt die magische Konstante 15, deswegen ist man reich an Information.
Verlier die Vier! / Aus Fünf und Sechs, / So sagt die Hex’, / Mach Sieben und Acht, / So ist’s vollbracht:
Die zweite Reihe enthält also 0, 7 und 8. Die dritte Zeile muss zwangsläufig die 5, die 6 und die “verlorene 4” enthalten.
Und Neun ist Eins / Und Zehn ist keins. / Das ist das Hexeneinmaleins!
Es gibt – wie hier die Verse Goethes gedeutet werden – zwar ein fastmagisches Quadrat mit 9 Zahlen, aber keines mit 10, weil 10 keine Quadratzahl ist.
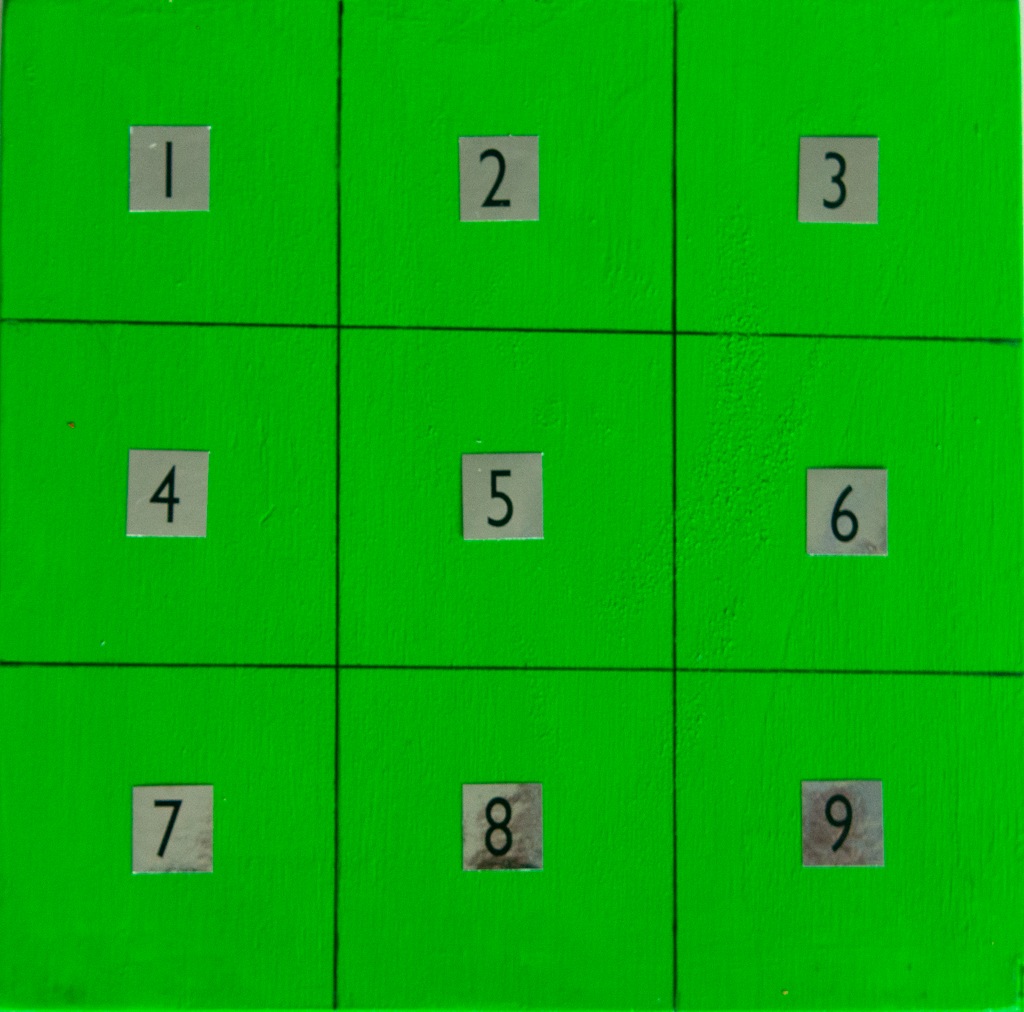

Ein weiteres magisches Quadrat, das aus der Renaissance stammt, das sehr berühmt ist und voller Symmetrien steckt, befindet sich auf einem der besten Kupferstiche von Albrecht Dürer, ein nicht leicht zu interpretierendes Bild mit dem Titel Melencolia I.
In der Mathothek gibt es ein Exponat zu diesem magischen Quadrat der Ordnung n=4:



Die magische Konstante dieses Quadrats beträgt 34, die zu verteilenden Zahlen sind die von 1 bis 42=16
Neben dem Entstehungsjahr 1514 des Stichs gibt es auch noch einen Hinweis auf den Schöpfer: In den beiden unteren Ecken stehen die Zahlen 4 und 1. Stellt man eine Beziehung zum Alphabet her, dann ist der vierte Buchstabe D und der erste natürlich A, also die Anfangsbuchstaben des Namens Dürer Albrecht, mit denen er seine Werke signierte.
Das Dürer-Quadrat weist noch mehrfach die magische Konstante 34 auf, z.B. in jedem Eckquadrat ergeben die vier Zahlen die Summe 34, ebenso ist die Summe der vier Zahlen um den Mittelpunkt 34. Es addieren sich aber auch die Zahlen 3, 8, 14 und 9 zu 34, die die Ecken eines Quadrats im Grundquadrat bilden. Dasselbe gilt für die Zahlen 5, 15, 12, 2. Die beiden Quadrate hängen durch eine Spiegelung zusammen. Mithilfe von Symmetrien entdeckt man weitere Auftritte der magischen Konstanten, z.B. bei den Zahlen 3, 2, 15 und 14, sowie bei den Zahlen 3, 2, 15, 14. Für die weitere eigene Suche: Waidmanns Heil! Durch die vielen symmetrischen Eigenschaften (Achsenspiegelungen an den Seitenhalbierenden und Diagonalen sowie Drehungen am Mittelpunkt um 90°, 180° und 270°) lassen sich weitere magische 4×4-Quadrate erstellen, die aber nicht wesentlich verschieden sind.
Wenn man im magischen Quadrat von Dürer verschiedene Möglichkeiten der magischen Summe durch Linien verbindet, erhält man interessante und ästhetische Muster. In dem gezeigten Beispiel verbinden die verschiedenen Quadrate bzw. Parallelogramme jeweils vier Zahlen, die addiert die magische Konstante liefern.


In dem kleinen Kästchen mit den Teilen des Dürer-Quadrats befinden sich auch die Bausteine für ein weiteres berühmtes Quadrat. Allerdings handelt es sich dabei nur um ein fastmagisches Quadrat.

Es stammt von dem Architekten Gaudi und seiner Kirche Sacrada Familia in Barcelona: In jeder Spalte, jeder Zeile und jeder Hauptdiagonalen beträgt die Summe der eingetragenen Zahlen 33, und damit das angenommene Alter von Jesus Christus bei seiner Kreuzigung. Es handelt sich hier dennoch um kein echtes magisches Quadrat, da die Zahlen 10 und 14 doppelt vorkommen und dafür die Zahlen 12 und 16 fehlen.
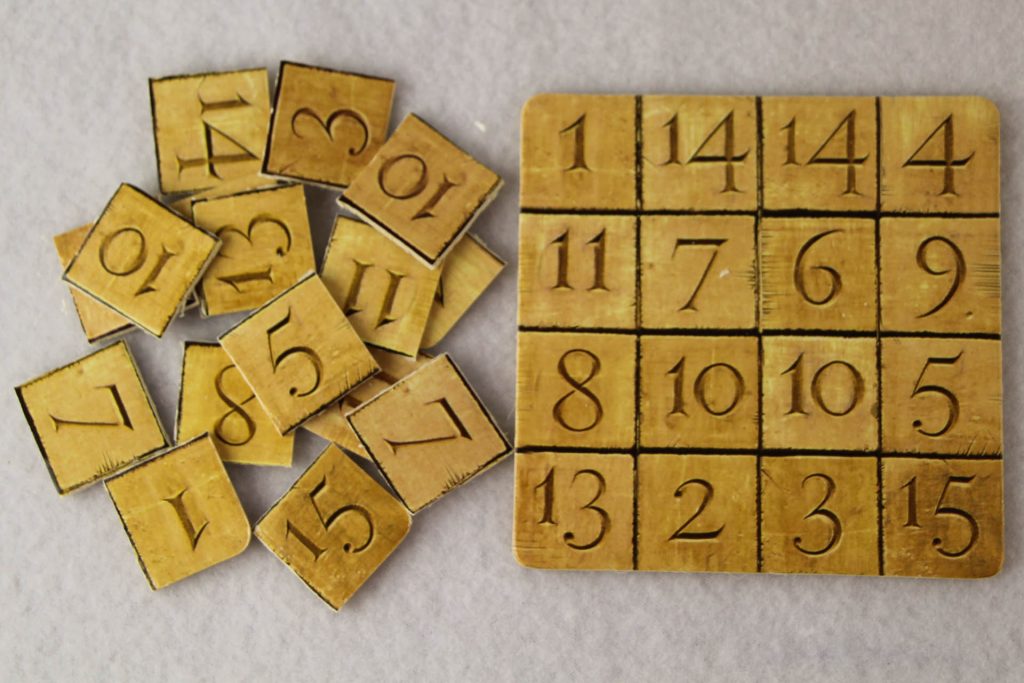
Es gibt noch ein weiteres aus edlen Hölzern gemachtes 4×4 Quadrat mit den Zahlen von 0 bis 15, die zu einem magischen Quadrat angeordnet werden können.


Die verdeckte Rückseite dieses magischen Quadrates zeigt ein schönes griechisch-lateinisches Quadrat mit vier schwarzen Symbolen Sonne, Mondsichel, Vollmond und Stern auf den vier unterschiedlich dunklen hölzernen kleinen Quadraten. Dass die vier Holzarten ein lateinisches Quadrat bilden, ist auch auf dieser Seite zu erkennen.
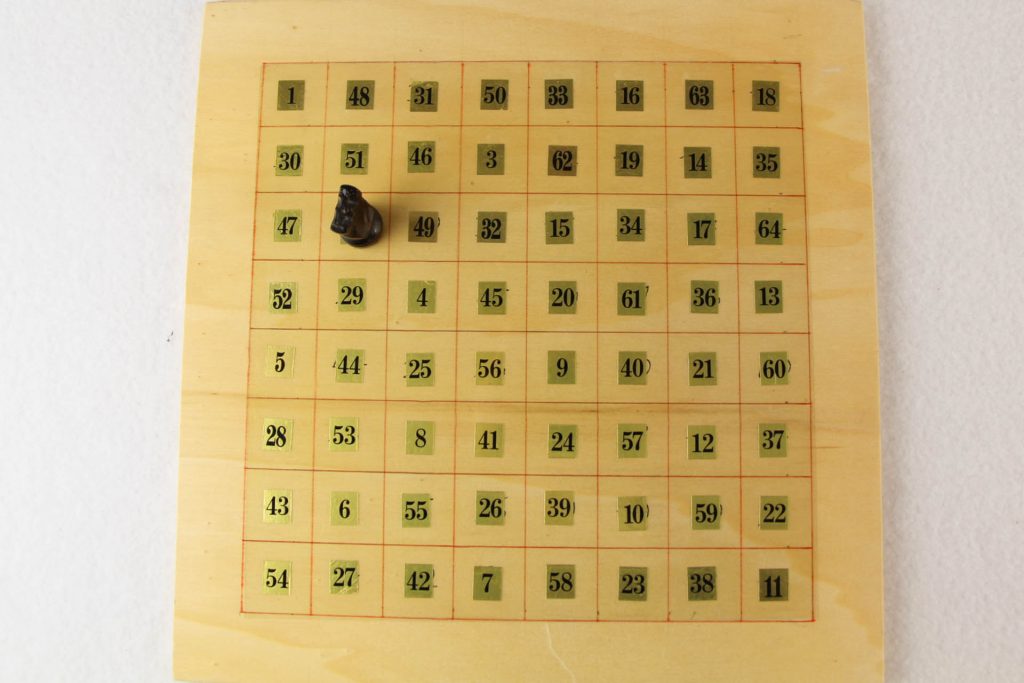
Bei dem nächsten Zahlenquadrat handelt es sich um ein interessantes, aber nur um ein “fast-magisches” 8×8-Quadrat, bei dem zwar die Summe der Zahlen jeder Zeile und jeder Spalte 260 beträgt, aber die Zahlen der beiden Hauptdiagonalen erfüllen diese Bedingung allerdings nicht und insofern handelt es sich hier um kein echtes magisches Quadrat.
Die Zahlen 1 bis 64 sind andererseits so auf dem Brett platziert, dass man mit der Spielfigur des Springers die Zahlen von 1 bis 64 im Rösselsprung durchlaufen kann. Der Rösselsprung ist beim Schach der Zug des Springers: ein Feld in gerader und ein Feld in schräger Richtung oder umgekehrt.

Das folgende Objekt soll ein besonderes magisches Quadrat der Ordnung n=4 werden. Als zusätzliche Bedingung müssen die Zahlen so eingesetzt werden, dass in jedem 2×2-Quadrat die Summe der vier Zahlen ebenfalls die magische Konstante 34 liefert.

Die Lösung sieht dann so aus:

Die Zahlen 8, 1, 10 und 15 im linken oberen Eckquadrat ergeben bei ihrer Addition 34, die Zahlen 15, 4, 6 und 9 des Quadrats in der Mitte ergeben auch 34 und ebenso 6, 9,12 und 7 im mittleren unteren Quadrat. Alle 2×2-Teilquadrate ergeben die magische Konstante 34. Ein magisches Quadrat mit dieser Eigenschaft nennt auch “all-diagonal“.
Die folgenden vier magischen Quadrate der Ordnung 4 sind solche all-diagonalen Exemplare. Dabei treten insgesamt die Zahlen von 1 bis 64 auf. Die magische Konstante beträgt bei jedem der vier Quadrate 130.

Setzt man diese vier Quadrate zu einem 8×8-Quadrat zusammen, so erhält man wieder ein allmagisches Quadrat mit den Zahlen 1 bis 64 und der magischen Konstanten 130⋅2=260, das z.B. so aussehen kann:

Das größte magische Quadrat, das in der Mathothek präsentiert wird, ist das von dem Erfinder des Blitzableiters und einem der Gründerväter der USA erfundene und nach ihm benannte Benjamin Fränklin-Quadrat. Seine innere Struktur ist nach dem Kennenlernen des vorigen allmagischen Quadrats besser zu verstehen.

Dieses Zahlenquadrat mit 16×16 Feldern wurde von Benjamin Franklin (1706 – 1790) ausgetüftelt. Dieser frühe Politiker der USA – einer ihrer Gründerväter – und Physiker, der als solcher auch durch die Erfindung des Blitzableiters berühmt wurde, hat sich hier ein besonderes fastmagisches großes und interessantes Quadrat ausgedacht. (Vielleicht als psychischer Blitzableiter?)
Eigenschaften des Franklin-Quadrates:
- Die Summen der Zahlen jeder Zeile und jeder Spalte sind gleich, nämlich der magischen Konstanten 2056
- Die Summen der Zahlen der halben Zeilen und halben Spalten sind immer gleich, und zwar der Hälfte der magischen Konstanten 1028
- Die Summen der Zahlen in jeder der beiden Hauptdiagonalen sind beide gleich 2184, aber somit nicht gleich der magischen Konstanten
- Die Summen der Zahlen von jeder halben Hauptdiagonalen beträgt die Hälfte der Summe der ganzen Diagonalen, d.h. 1092
- Die Summe der vier Zahlen in jedem 2×2-Teilquadrat ist eine feste Zahl, die gleich dem Vierfachen der Konstanten geteilt durch die Anzahl der Spalten ist, also 4×2056:16=514. Das ist ein Viertel der magischen Konstanten.
Die Konstruktion und die zusätzlichen Herausforderungen magischer Quadrate führen zu einer Fülle von Denkaufgaben und mathematischer Unterhaltung. In der Mathothek gibt es noch eine Menge solcher Knobeleien, die aus der Idee des magischen Quadrats erwachsen sind. So beispielsweise sind aus der Kombination von magischem Quadrat und Geometrie die verschiedenen Varianten der geomagischen Quadrate entstanden.
In der Mathothek gibt es noch viele weitere Varianten von Knobeleien mit der Idee des magischen Quadrats. Dazu werden die Regeln des magischen Quadrats unter Beibehaltung wesentlicher Merkmale reduziert, erweitert und abgeändert: “Das magische Quadrat und interessante Abwandlungen für anspruchsvolles Gehirnjogging”.