Wie können wir helfen?
Wie lässt sich anschaulich der Zusammenhang von Flächeninhalt und Umfang eines Kreises bestimmen?
Teilt man die Kreisfläche in vier gleich große Kreissegmente und legt diese wie oben nebeneinander, kann man noch nicht viel damit anfangen…
Anders sieht es schon aus, wenn die Kreisfläche in acht gleich große Segmente unterteilt wird. Hier kann man grob angenähert ein Parallelogramm erkennen.
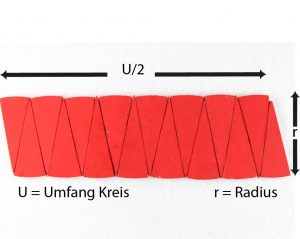
Die Aneinanderreihung von sechzehn gleich großen Kreissegmenten lässt das Parallelogramm bereits recht gut erkennen.
Zumindest gedanklich lässt sich dieser Prozess immer weiter fortsetzen und verstärkt die richtige Vermutung, dass der Flächeninhalt A des Kreises, mit dem Radius r, gleich dem Flächeninhalt des Parallelogramms, mit der Länge des halben Kreisumfangs (½ · U) und der Breite (r), ist, also A = ½ · U · r gilt.
Die grünen Kreisscheiben mit den aufgemalten Durchmessern sowie die Holzringe dienen zusammen mit dem Maßband zur experimentellen Erfassung des Zusammenhangs von Kreisumfang und Durchmesser.
Hierzu nimmt jeweils eine der grünen Kreisscheiben und ein biegsames Maßband, misst die Länge des schwarzen Durchmessers der grünen Kreisfläche und die Länge des Kreisumfangs. Anschließend dividiert man die Länge des Umfangs durch die Länge des Durchmessers. Dieses Experiment liefert dann mehr oder weniger genaue Werte für das Verhältnis U:d. Beispielsweise erhält man im Falle des größten Kreises U=78,7 cm und d=25 cm und somit U:d=3,148. Bei zwei weiteren Messungen und Berechnungen erhalten wir U=62,8 cm und d=20 cm und damit U:d= 3,14 und für den kleinsten Kreis erhalten wir mit U=37,7 cm und d=12 cm das Verhältnis U:d=3.14166… , also in allen diesen Fällen erhalten wir ungefähr das gleiche Ergebnis, nämlich 3,14. Das Verhältnis von Umfang und Durchmesser eines Kreises bezeichnet man mit dem griechischen Buchstaben π (Pi). Mit ihm lassen sich Flächeninhalt und Umfang eines Kreises aus dessen Durchmesser leicht beschreiben:
1. Der Flächeninhalt A eines Kreises mit Durchmesser d: A=(d/2)2⋅π oder A=r2⋅π mithilfe des Radius r=d/2
2. Der Umfang U eines Kreises mit dem Durchmesser d oder dem Radius r U=d⋅π oder U=2⋅r⋅π
Um zu 1. zu kommen, gehen wir von der oben gemachten Erkenntnis über den Zusammenhang von Kreisumfang und Kreisfläche aus, dass A=1/2⋅U⋅r gilt und benutzen U=2⋅r⋅π, dann erhalten wir A=1/2⋅(2⋅r⋅π)⋅r. Daraus ergibt sich A=r2⋅π und mit r=d/2 auch A=(d/2)2⋅π.
Wie weit der Weg dann noch ist, zu den tiefen Geheimnissen des Verhältnisses von Flächeninhalt und Umfang eines Kreises bzw. deren Verhältnis zu ihrem Durchmesser bzw. Radius vorzudringen, deutet das folgende Bild in der Mathothek über die Zahl Pi an. Sicher ist auf jeden Fall, dass die Ziffern ihrer Nachkommastellen nie enden und ohne ein erkennbares Muster zu sein scheinen, das Licht in die Tiefen dieser Zahl brächte.