Wie können wir helfen?
Dieses farbig und flächenhaft gestaltete Bild in der Mathothek ist eine besonders ansprechende Darstellung der Koch’schen Schneeflockenkurve. Wie der Name schon sagt, ist das dahinterstehende Gebilde nur eindimensional. Es handelt sich bei der Schneeflockenkurve eigentlich nur um den Rand. Ursprünglich wurde sie als Beweis erdacht, um zu zeigen, dass in der reellen Analysis Stetigkeit nicht logischerweise die Differenzierbarkeit nach sich zieht, dass eine Kurve an jedem Punkt zwar stetig, aber nicht differenzierbar sein kann. Sie wurde so ein Mitglied des mathematischen “Zoos der Monsterfunktionen”.
Mathematisch betrachtet ist sie aber auch ein interessantes Beispiel für eine fraktale Struktur:
Fraktale Muster zeichnen sich durch ihre Selbstähnlichkeit aus. Bestimmte Formen des Ganzen wiederholen sich immer wieder im Detail.
Es gibt eine interessante Deutung des Bildes, wie es entstanden sein könnte. Diese Erklärung deckt dann den Zusammenhang dieses Bildes mit einem weiteren Sierpinski-Fraktal auf. Dabei spielen Hexagramme (regelmäßige sechseckige Sterne) eine wichtige Rolle. Wir beginnen mit sechs kleinen schwarzen Hexagrammen, ordnen sie zu einem Sechseck. Anschließend fügen wir sechs solcher Sterne zu einem großen Sechseck zusammen.
Im nächsten Schritt bedecken wir in diesem Muster je sechs zusammenhängende schwarze Sterne mit gelben Hexagramm:
Wir legen dann die beiden großen gleichseitigen Dreiecke so aufeinander, dass ein blau-rotes Hexagramm entsteht und legen das Ergebnis auf den schwarz-gelben Sternenkranz.
Das Ergebnis ist unser Bild von der Koch’schen Schneeflocke.
Natürlich können wir den Prozess auch als Entdeckungstour gestalten:
Bleibt am Schluss die Frage: Wie ist das Bild nun tatsächlich entstanden? So oder so oder doch ganz anders?
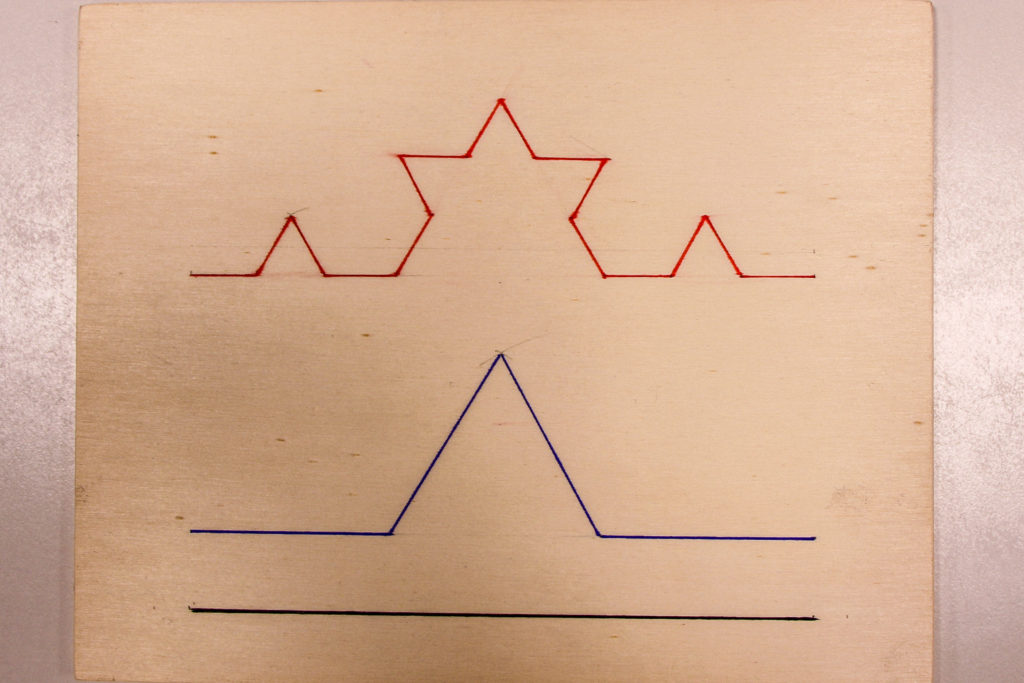
Betrachten wir nun nochmal die folgenden Bilder in dieser Abfolge:
Jetzt erkennen wir in dem Aufbau unseres Bildes die drei ersten Schritte eines Fraktals mit der Konstruktionsvorschrift, dass bei jedem Schritt die sechs Spitzen des Hexagramms durch ein entsprechend verkleinertes Hexagramm ersetzt wird. Dieses Fraktal hat den Namen Sierpinski-Sechseck.
In der Mathothek haben Entdecken und Kreativität eine Heimat und sind alle Menschen, die sich darauf einlassen, herzlich willkommen. Zum Thema Fraktale Geometrie gibt es hier noch viele Exponate, die informieren und anregen können, ergänzt durch “Wort und Bild” in unserem Katalog.










Ein sehr schöner alternativer Zugang zur Kochschen Schneeflocke. Ich finde es reizvoll, die Kinder selbst diese Figur durchs Legen entdecken zu lassen. Kann man die Vorlagen für die Sterne bekommen?