Wie können wir helfen?
Es fängt so harmlos an mit niedlichen Kätzchen und kleinen quadratischen Kärtchen:
Es sind neun gleich große Kärtchen oder Kacheln, auf denen “halbe” Katzen zu sehen sind. Mal befindet sich ein Oberteil und mal ein Unterteil einer Katze über den vier Seitenkanten der Karte. Dabei handelt es sich um verschiedene Katzen. Und hier steckt das Problem: Die Kärtchen müssen nämlich so aneinandergelegt werden, dass die beiden “Katzenhälften” zweier benachbarter Karten eine einzige ganze Katze ergeben.
Hier ein erster Schritt die neun Karten zu einem Quadrat zu legen, Dabei stellt man fest, dass noch keine zwei benachbarten Kacheln gemeinsame Kanten haben.
Deswegen solltest Du jetzt zunächst mit folgenden vier Karten ein 2×2-Quadrat legen, bei dem jedes Paar Kacheln mit gemeinsamen Kanten sich stimmig ergänzt. Die vier Kärtchen sind auf der Rückseite mit einem blauen Punkt markiert:
Auch bei den anderen Kachel-Puzzlen sind jeweils vier Kacheln mit einem blauen Punkt gekennzeichnet, aus denen sich ein solch stimmiges 2×2-Quadrat legen lässt. Vielleicht probst Du hier Dein Können oder Glück, vielleicht auch mit Freunden oder Freundinnen? Jeder sollte seine Zeit festhalten, die er für die Lösung der Aufgabe braucht.
Hier ist das gesuchte 2×2-Quadrat, das aus den vier mit blauem Punkt markierten Kacheln gelegt werden soll:
Nun steht die schwierigere Herausforderung an: Mit allen neun Kacheln ein 3×3-Quadrat zu legen. Dabei kann man natürlich die oben gemachte Erfahrung benutzen.
Nach einigem Ausprobieren und klugen Überlegungen gelingt das große 3×3-Quadrat, bei dem alle Kacheln so angeordnet sind, dass die Katzenteile zu hübschen Kätzchen zusammengesetzt sind. Hier ist die Lösung:
Jetzt solltest Du vielleicht ohne Hilfe versuchen, die Aufgabe selbst zu lösen. Nach dem Katzen-Puzzle kannst Du es mit den vier anderen Kachel-Puzzlen versuchen. Dabei sollte die Zeit festgehalten werden, die Du brauchst oder Deine Mitspieler brauchen, um jeweils die Aufgabe zu lösen.
Hier sind die anderen vier Kachel-Puzzlen der Mathothek mit ihren verschiedenen Motiven:
Das r-Spiel:
Das Hexen-Puzzle:
Das Bibi-Blocksberg-Puzzle:
Das Noch-verzwickter-Puzzle:
Die Lösungen dieser vier Kachel-Puzzlen sind ganz am Ende dieses Artikels zu finden.
In dem interessanten und gut verständlichen Buch Abenteuer Informatik von Jens Gallenbacher findet man im Zusammengang mit einem weiteren Kachel-Puzzle – Affenpuzzle – eine Erklärung von nicht praktisch lösbaren Problemen und damit eine prinzipielle Verneinung der Frage, ob der Computer allmächtig ist.
Die oben gezeigten Kachel-Puzzles, die den Besuchern zur Verfügung stehen, sollen natürlich zuerst Spaß machen, herausfordern, die Konzentration und die Ausdauer stärken, das intelligente Ausprobieren fördern. Den Abschnitt Allmächtiger Computer!? in dem Buch von Jens Gallenbacher lohnt es sich intensiv zu lesen. Er erklärt darin, was man in der Informatik als ein nicht praktisch lösbares Problem bezeichnet. Danach zeigt er mit einem weiteren Affen-Puzzles streng logisch, dass der Computer zwar ein sehr leistungsfähiges und zuverlässiges Werkzeug für den Informatiker ist, dass er aber nie in der Lage sein wird, Antworten auf alle sinnvollen Fragen zu geben, die die Informatiker in ihrem Bereich stellen.
Wenn man die durchschnittlichen Zeiten betrachtet, die zur Lösung eines neuen Kachel-Puzzles benötigt wird, so ist es für die meisten sehr überraschend, dass man für ein 2×2-Quadrat etwa nur wenige Minuten braucht, aber für das 3×3-Quadrat schon etwa eine Stunde, obwohl die Kartenzahl sich fast nur verdoppelt hat. Für ein 4×4-Quadrat braucht man wesentlich mehr Zeit als zwei Stunden – wenn man es überhaupt schafft. Ein 5×5-Quadrat schaffen nur die wenigsten Menschen, und dass auch nur mithilfe eines Computers und höchst intelligentem Ausprobieren. Bisher sieht es so aus, dass mit jeder weiteren Vergrößerung der Zahl der Puzzleteile für die Aufgabenlösung sehr erheblich viel mehr Lösungszeit erforderlich wird. Wenn bei einem lösbaren Problem mit jedem weiteren Puzzleteil die notwendige Lösungszeit absurd lange dauert und somit das Problem unlösbar wird, nennt man das ein nicht praktisch lösbares Problem. Bisher ist es noch nicht bewiesen, dass das Kachel-Puzzle-Problem tatsächlich zu den praktisch nicht lösbaren Problemen gehört. Aber bisher sind aber auch alle Versuche gescheitert, einen pfiffigen Algorithmus zur Lösung zu finden.
Geht man davon aus, dass es sich hier bei dem Kachel-Puzzle-Problem um solch ein nicht praktisch lösbares handelt, wird man bei konkreten Kachel-Puzzlen nicht ohne eine Portion intelligentem strategischem Ausprobieren zu einer Lösung kommen können. Ein sinnvolles Vorgehen entspricht dem Branch and Bound-Prinzip in der Informatik, d.h. dass man möglichst frühzeitig erkennt, dass man beim Ausprobieren einen definitiv falschen Zweig erreicht hat und umkehren muss. Aber auch diese Strategie reicht nicht, um das 6×6- und das 7×7-Quadrat “in nicht absurd langer Zeit” zu lösen. Also bleibt es auch trotz dieser “Verzweigungs- und Schranken-Strategie” ein praktisch nicht lösbares Problem.
Ein weiteres Puzzle, das aus blauen und rosa Affen-Kacheln besteht , die nach Vorlagen des Informatikbuches in der Mathothek hergestellt wurden, macht interessante Entdeckungen möglich:
Interessant ist hier die folgende Aufgabe: Kann man mit den drei verschiedenen blauen Kacheltypen, bzw. mit den drei rosa Kacheltypen die gesamte unendliche Ebene regelkonform parkettieren?
Dass das für die blaue Serie gelingen kann, sieht man am gelungenen Beispiel. Da die obere Kante dieses Quadrates und die untere regelgemäß aneinander passen, ebenso die linke und die rechte Kante zueinanderpassen, liegt ein Grundquadrat vor, mit dem sich die ganze unendliche Ebene regelgerecht pflastern lässt.
Ganz anders sieht es mit den rosafarbenen Kacheln aus:
Hier gibt es definitiv beweisbar keine solche Möglichkeit.
Hier ein erster Versuch:
Dass auch jeder weitere Versuch scheitern muss, lässt sich beweisen, ohne alle möglichen 3×3-Quadrate ausprobieren zu müssen. Zunächst stellt man fest, dass sich die drei Typen der rosa Kacheln nur so legen lassen, wie es unten in der ersten senkrechten Reihe zu sehen ist. Diese ließe sich nach unten und auch nach oben unendlich periodisch fortsetzen. Aber beim Anlegen einer zweiten solchen Reihe, die ja dieselbe Periode aufweisen würde, zeigt sich, dass es keine regelkonforme Möglichkeit gibt. Damit ist klar, dass weder ein Quadrat noch irgendein anderes Rechteck mit den rosa Kacheln in der gewünschten Form gelegt werden kann.
Das nächste Foto zeigt nun einen Ausschnitt aus einem aperiodischen Kachelmuster, dass sich unendlich fortsetzen lässt, also die gesamte Ebene überdeckt:
Mit der Erfahrung, die wir mit den rosa und blauen Affen-Kacheln gemacht haben, ist man auch hier versucht, ein Grund-Quadrat oder -Rechteck zu suchen, das passende Seiten besitzt. Natürlich lässt sich in dem obigen kleinen Ausschnitt des unendlichen Puzzles mit Fleißarbeit durch Überprüfung aller in diesem oder auch jedem anderen Ausschnitt denkbaren Rechtecke zeigen, dass keines dieser Rechtecke passende Kanten besitzt, aber auch kein Legefehler vorliegt. Für einen Computer mit der geeigneten Software wäre diese Aufgabe gut lösbar. Der korrekte Beweis dafür, dass die obige Parkettierung in ihrer unendlichen Ausdehnung kein einziges passendes Rechteck besitzt, aber doch eine regelgerechte Kachelung ist, würde hier den Rahmen sprengen.
Würde man nun ein Programm schreiben, das für einen Satz Kacheln und eine unendliche Parkettierung untersucht, ob ein Rechteck mit passenden Seiten existiert und kein Legefehler vorhanden ist, so träte im Fall unserer aperiodischen unendlichen Kachelung Erstaunliches zutage. Falls der Computer ein solches passendes Rechteck findet und keinen Legefehler vorliegt, so soll die Antwort
→JA
und im anderen Fall
→NEIN
lauten.
Es ist zunächst plausibel, dass der Computer irgendwann in endlicher Zeit ein JA oder ein NEIN ausspuckt. In dem Fall der obigen aperiodischen Kachelung käme nie ein JA oder NEIN, sondern der “elektronische Sklave” würde “ewig” weiterrechnen. Da diese aperiodische Kachelung einerseits kein passendes Rechteck enthält, aber andererseits auch keinen Legefehler aufweist, sucht der Computer immer weiter, ohne sich zwischen JA oder NEIN entscheiden zu können. Den Beweis dafür, dass dieses aperiodische Parkett diese Eigenschaften – fehlerfrei und ohne geeignetes Rechteck zu sein – besitzt, konnte nur einem Menschen mit seiner kreativen Intelligenz gelingen. Natürlich gäbe es aufgrund dieses genialen Beweises die Möglichkeit, die Software für diesen Fall anzupassen. Aber was ist mit weiteren möglichen Fällen, die vielleicht noch keinem Menschen bekannt sind? Solche Probleme sind nicht nur praktisch nicht lösbar, sondern vom Computer grundsätzlich nicht entscheidbar. Letztlich lässt sich rein logisch beweisen, dass es nie einen Computer geben wird, der die Antwort auf jede sinnvolle Frage der Informatik liefern kann. Einige Problemlösungen können nur mit den schöpferischen Kräften des Menschen – wenn überhaupt – gelöst werden, weil entweder Computer zu viel Zeit brauchen werden oder Computer prinzipiell dazu nicht in der Lage sind.
Es gehört zu den faszinierendsten Fortschritten in der Mathematik und auch der Informatik, dass sie ihre prinzipielle Begrenztheit beweisen können.
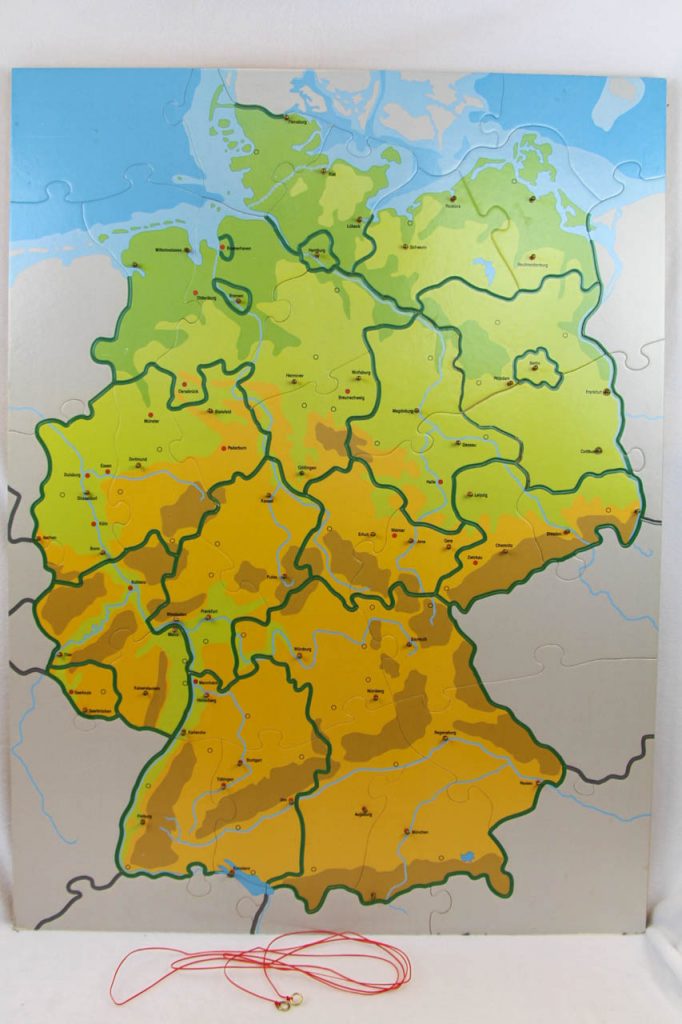
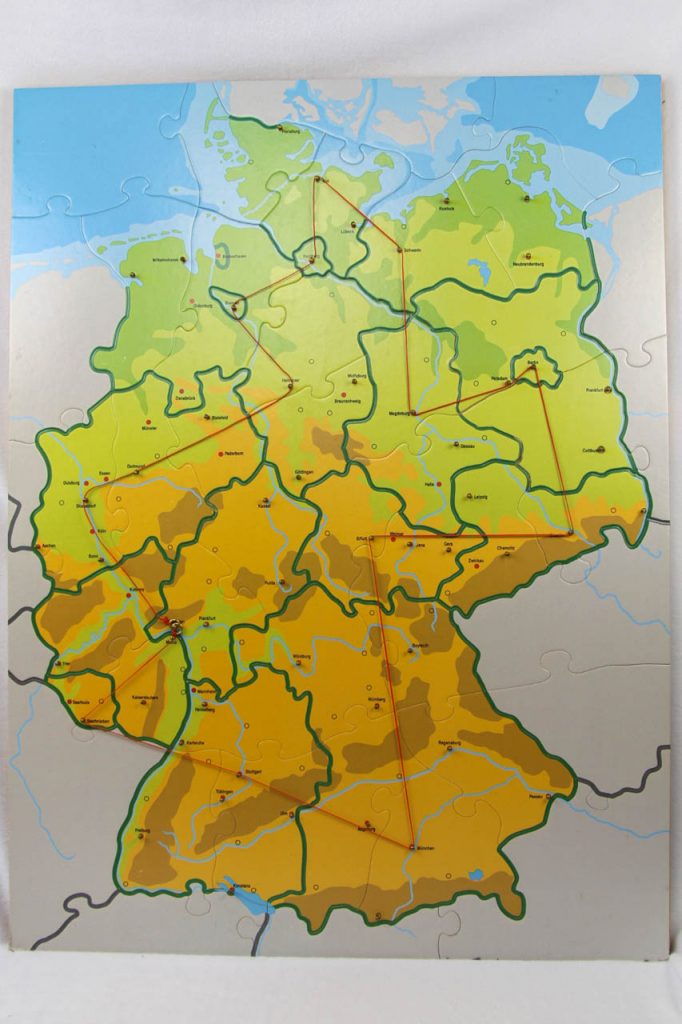
In der Mathothek gibt es ein weiteres Exponat zum Thema nicht praktisch lösbare Probleme, die kürzeste Rundreise durch deutsche Städte.
Für Leute, die noch Lust auf mehr Legespiele und Kachel-Puzzlen haben, gibt es in der Mathothek noch jede Menge Herausforderungen, dass es schon zu einem “nicht praktisch lösbaren Problem” werden könnte, sie alle kennenzulernen und natürlich auch zu lösen. Hier einige Beispiele:
Lösungen der Kachel-Puzzles: