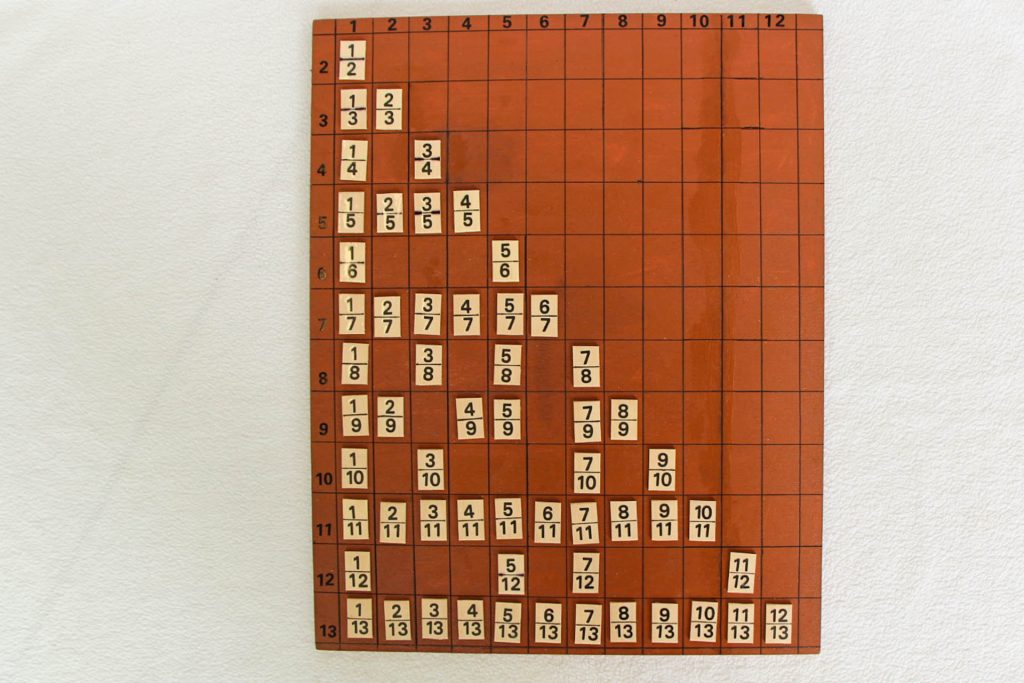Wie können wir helfen?
Da scheint die Antwort sofort auf der Hand zu liegen. Allein zwischen 0 und 1 liegen schon unendlich viele Bruchzahlen. Das ist auch nicht schwierig einzusehen: Nimmt man von zwei Bruchzahlen, die zwischen 0 und 1 liegen, das arithmetische Mittel, dann ist das Ergebnis wieder eine Bruchzahl zwischen 0 und 1 mit demselben Abstand von beiden Ausgangszahlen. Gäbe es nun nur endlich viele Bruchzahlen zwischen 0 und 1, so würde man durch Bildung des arithmetischen Mittels zweier vorhandener Bruchzahlen immer wieder neue Bruchzahlen erzeugen können. Das widerspricht der Annahme, also muss es unendlich viele Bruchzahlen zwischen 0 und 1 geben. Es kann daher auch keine Lücken zwischen irgend zwei Bruchzahlen geben, denn das arithmetische Mittel dieser beiden Bruchzahlen liegt dann in der “Lücke”.
Vergleichen wir nun die beiden Mengen, die Menge der nicht negativen rationalen Zahlen (Menge der Bruchzahlen) und die Menge der natürlichen Zahlen, so haben beide Mengen unendlich viele Elemente. Aber andererseits sind alle natürlichen Zahlen auch Bruchzahlen, nicht aber alle Bruchzahlen auch natürliche Zahlen. Die Menge der natürlichen Zahlen ist also in der Menge der Bruchzahlen als echte Teilmenge enthalten. Insofern gibt es “mehr” nicht negative rationale als natürliche Zahlen.
Enthält eine Menge M1 in diesem Sinne “mehr” Elemente als eine Menge M2, gilt also, dass M2 eine echte Teilmenge von M1 ist, dann sagt unser gesunder Menschenverstand, dass auch die Anzahl der Elemente von M1 größer sein müsste als die Anzahl der Elemente von M2. Für Mengen mit endlich vielen Elementen ist das auch vollkommen richtig.
Nun sind aber unsere beiden Zahlenmengen keine endlichen Mengen. Deshalb müssen wir hier die “Anzahl” der Elemente beider Mengen abzählen. Wir müssen einen Weg finden, wie wir die Elemente der beiden Mengen einander umkehrbar eindeutig zuordnen können. Als leicht verständliches Beispiel soll die Menge M1= Menge der natürlichen Zahlen und M2= Menge der Quadratzahlen sein. Dann ist sofort klar, dass es “mehr” natürliche Zahlen als Quadratzahlen gibt, schließlich ist jede Quadratzahl auch eine natürliche Zahl, aber das Umgekehrte gilt nicht, d.h. M2 ist eine echte Teilmenge von M1. Dabei erkennt man dann auch sehr leicht, dass es eine einfache umkehrbare Zuordnung zwischen den Elementen der beiden Mengen gibt: n↔n2 für n=0, 1, 2, 3, usw. Beispielsweise gehört zu der natürlichen Zahl 13 die Quadratzahl 169, zur Quadratzahl 121 die natürliche Zahl 11.
Der deutsche Mathematiker Georg Cantor (1845 – 1918), der sich in seiner Mengenlehre grundlegend mit dem Unendlichen auseinandergesetzt hat, führte den Begriff der abzählbar unendlichen Menge ein. Sie beschreibt die erste Stufe von Unendlichkeiten. Dabei ist eine Menge abzählbar unendlich oder enthält abzählbar unendlich viele Elemente, wenn sich diese umkehrbar eindeutig den natürlichen Zahlen zuordnen oder alle in einer Reihenfolge hintereinander in einer Liste aufschreiben oder sich “nummerieren” lassen (natürlich nur gedanklich, aber prinzipiell). Demnach sind z.B. die Mengen der Quadratzahlen, der durch drei teilbaren Zahlen, aber auch die Menge der ganzen Zahlen abzählbar.
Im Hinblick auf unendliche Mengen ergeht es uns wie Kindern, die noch keine Zahlen beherrschen. Soll ein solches Kind beispielsweise 12 Äpfel aus einem Vorrat holen, kann man ihm z.B. 12 Hölzchen geben und den Auftrag, für jedes Hölzchen einen Apfel zu nehmen und die Äpfel zu bringen. Durch diese Zuordnung von Hölzchen zu Äpfeln gelingt es dem Kind, genau 12 Äpfel zu bringen, auch ohne zählen zu können. Statt Mengen von Hölzchen zu nehmen, benutzen wir die handlichen natürlichen Zahlen.
Dass die Menge der Bruchzahlen, die zwischen 0 und 1 liegen, abzählbar ist, hat Georg Cantor 1874 in seinem ersten Diagonalverfahren gezeigt. Um diese einfache und geniale Idee zu verstehen benutzen wir das Exponat aus der Mathothek.
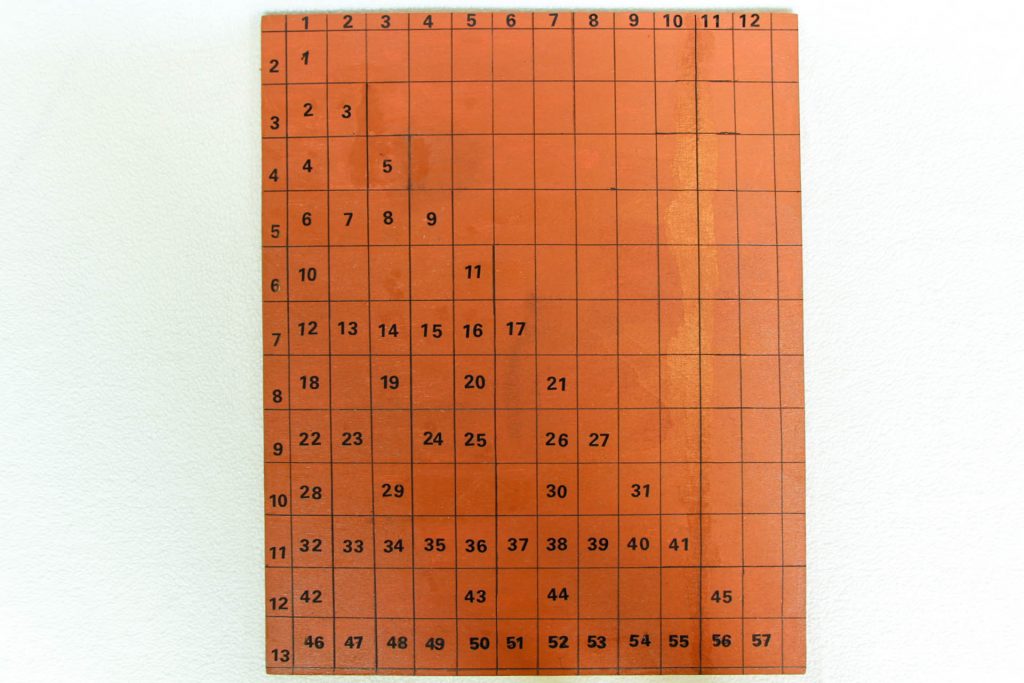
Da sich die Bruchzahlen nicht wie die natürlichen oder die Quadratzahlen nach ihrer Größe nummerieren lassen, benutzen wir jeweils die Grunddarstellungen der Bruchzahlen und ordnen diese dann nach der Größe ihrer Nenner. So bekommt 1/2 die Nummer 1, 1/3 die Nummer 2, 2/3 die Nummer 3, 1/4 die Nummer 4, 3/4 die Nummer 5. 2/4(=1/2) ist keine Grunddarstellung und fällt raus, um keine Bruchzahl doppelt zu zählen. Ein Bruch, bei dem Zähler und Nenner nur eins als gemeinsamen Teiler haben, nennt man Grunddarstellung. Auf diesem Weg lassen sich nicht nur die Bruchzahlen in dem Plastikkästchen beispielhaft nummerieren, sondern prinzipiell alle entsprechenden Bruchzahlen zwischen 0 und 1.
Anhand dieser Beispiele erkennt man das Prinzip der Zuordnung der Bruchzahlen zwischen null und eins zu den natürlichen Zahlen.
Durch weitere Überlegungen kann man auch zeigen, dass die Menge aller positiven rationalen Zahlen und sogar die Menge aller rationalen Zahlen abzählbar ist. Anders verhält es sich bei der Menge aller reellen Zahlen, denn ebenfalls im Jahr 1874 gelang es Cantor auch zu beweisen, dass die Menge aller reellen Zahlen nicht abzählbar unendlich ist, sondern “überabzählbar”. Dieser Beweis gelang ihm mit dem sog. zweiten Cantor’sche Diagonalverfahren. Es beruht ebenfalls auf einer ebenso einfachen wie genialen Idee, über die Du in einem weiteren Artikel mithilfe eines anschaulichen Exponats mehr erfahren kannst.