Wie können wir helfen?
Bei Dobble-Spielen geht es darum, dass ein Spieler möglichst schneller als die anderen Spieler Gleichheiten und Unterschiede bezüglich Form und Farbe erkennen und benennen kann. Das Spielset, das in der Mathothek zur Verfügung gestellt wird, besteht aus 30 runden Karten, die jeweils sechs hinsichtlich ihrer Form, Farbe oder Größe unterscheidbare Symbole zeigen.

In fünf Spielvarianten geht es dann darum, als Erster auf zwei vorgelegten Karten das gleiche Symbol zu finden und zu benennen. Je zwei der 30 Karten besitzen genau ein in Farbe und Form übereinstimmendes Symbol, d.h. auf irgend zwei Karten des Spiels gibt es immer ein und auch nur ein Symbol, bei dem Form und Farbe übereinstimmen. Hinsichtlich ihrer Größe dürfen sie sich unterscheiden.
Warnung an alle Erwachsenen: Ähnlich wie bei Memoriespielen haben auch bei diesem Spiel Kinder nach einiger Übung fast immer die größeren Chancen zu gewinnen!
Zwei Bilder zur Definition des gemeinsamen Elements und zum besseren Verstehen gleichwertiger Symbole:

Hier muss man den orangen Kreis als einziges gemeinsames Element erkennen und benennen, weil er das einzige Element ist, bei dem Form und Farbe übereinstimmen. Die unterschiedliche Größe spielt laut Spielregeln keine Rolle. Bei der Sieben ist die Form und die Größe gleich, aber die beiden Merkmale begründen keine relevante Übereinstimmung.

Bei dem nächsten Paar ist das gemeinsame Symbol die orange Acht, Form und Farbe stimmen überein. Das alleine ist schon hinreichend, die zusätzliche Übereinstimmung hinsichtlich der Größe ist für das Spiel unerheblich.
Während dieses Spiel käuflich zu erwerben ist, ist das zweite ein Unikat, das Frau Dr. Knoche sich speziell für die Mathothek ausgedacht und hergestellt hat.
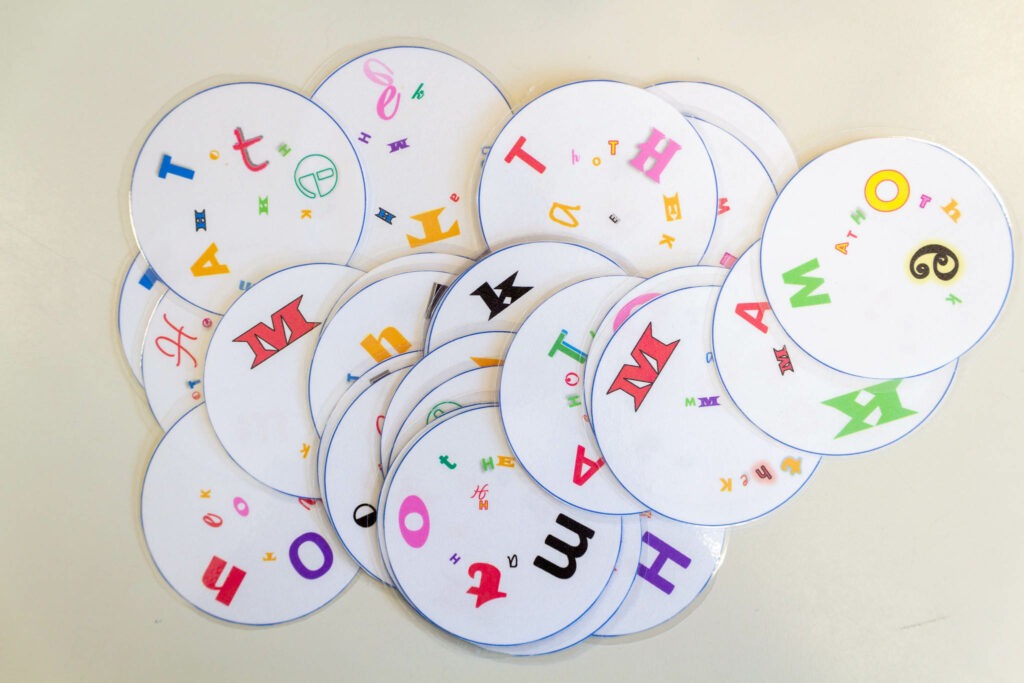
Jede der Scheiben enthält in verschiedenen Formen, Farben und Größen die Buchstaben, die in dem Wort “Mathothek” vorkommen. Für das Spiel selbst kommt es hier aber nur auf die groß geschriebenen Buchstaben an. Die klein geschriebenen Buchstaben sind Füllbuchstaben – gewissermaßen für das Spiel eigentlich überflüssig und nur Zierde – um auf jeder Karte alle Buchstaben des Wortes MATHOTHEK zu haben.
Hier zwei Beispiele:

Das einzige gemeinsame Symbol ist deutlich zu erkennen. Es ist natürlich das rote M. Beide entscheidenden Merkmale, Form und Farbe, stimmen überein. Dass auch beide Symbole die gleiche Größe haben, ist richtig, aber nicht notwendig.

Beim zweiten Beispiel ist das Erkennen des gemeinsamen Symbols schon etwas schwieriger. Hier sind sie nicht gleich groß, haben aber dieselbe Form und Farbe. Es ist das grüne K!
Um den geometrischen Bezug des Spiels transparent zu machen, betrachten wir ein weiteres Experiment der Mathothek, das im ersten Moment in keinem Zusammenhang mit dem Kinderspiel zu haben scheint. Dazu stellen wir uns vor, sieben Personen sollen sieben Ausschüsse bilden, aber keine “Eine-Person-Gruppen”. Alle Arbeitsgruppen sollen vernetzt sein. Dazu wird folgendes Prozedere vereinbart. Jeweils drei Personen sollen eine Gruppe bilden und jede Person soll in drei Gruppen mitarbeiten. Wie man eine solche Verteilung der sieben Leute erreicht, soll anhand eines weiteren Experiments erläutert werden, das aus sieben Ringen mit jeweils drei Buchstaben besteht. Jeder Buchstabe steht für eine der sieben Personen. Die sieben Ringe stellen dann die sieben Arbeitsgruppen dar.
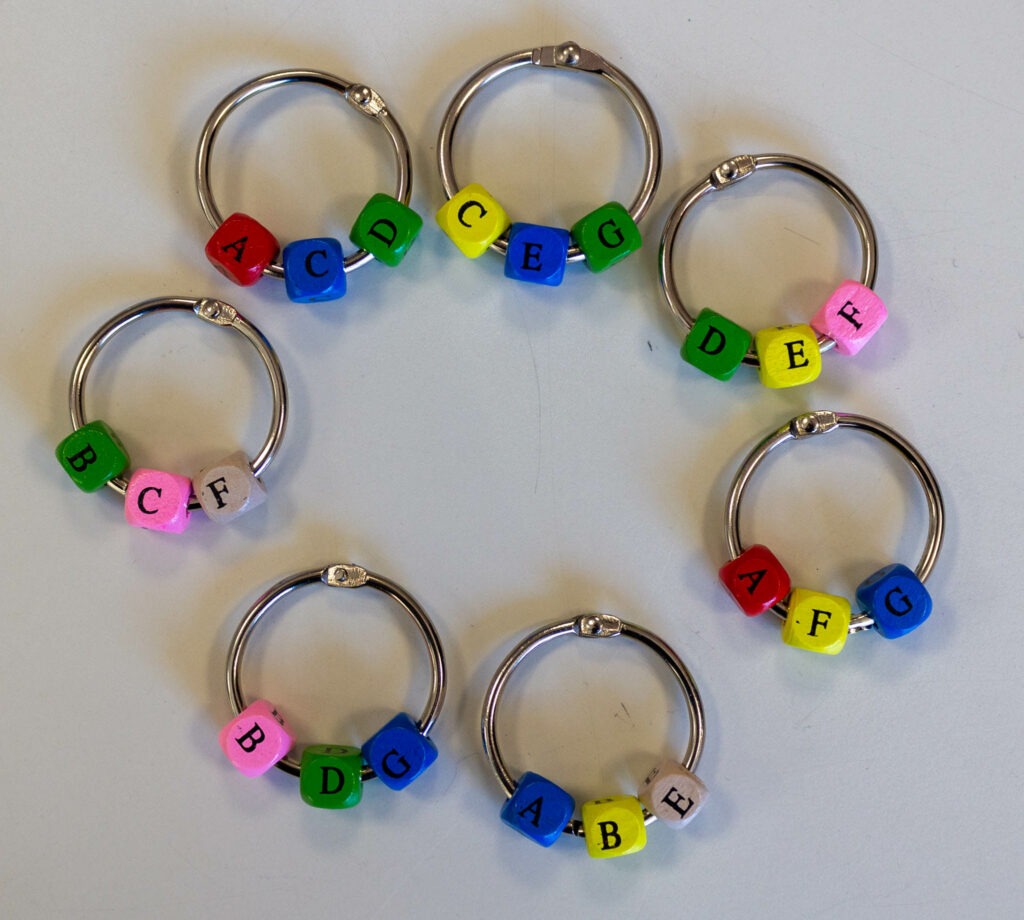
Und wir stellen erfreut fest, dass wir unsere Aufgabe der Arbeitsgruppenbildung gelöst haben. Wir übertragen das Ergebnis des “Ringexperiments” nun auf 21 Kärtchen:
Die 21 Kärtchen tragen auf der Vorderseite den Buchstaben (Namen) des Mitarbeiters und auf der Rückseite die Nummer der Gruppe, in der er mitarbeiten soll.








Dreht man die Kärtchen um, so sehen wir die Nummern der Arbeitsgruppen, in der die Person mitarbeiten wird.

Mit diesen 7 Ringen oder auch den 21 Kärtchen oder 7 Gruppen oder Kärtchenstapel können wir nun, nach dem die Arbeit erledigt ist, entweder ein sehr einfaches Dopple-Spiel spielen, (was allerdings ziemlich einfach und langweilig wäre) oder auch nach der gemeinsamen und damit nach der mathematischen Struktur fragen. Dazu legen wir eine Zeichnung an. Wir ordnen den Buchstaben A, B, C, D, E, F und G sieben verschiedene Punkte zu und verbinden sie mit sieben Geraden. Dann können wir uns leicht davon überzeugen, dass alle unsere Modelle sich hier dargestellt finden. Beispielsweise können wir die Punkte durch die Mitarbeiter ersetzen und die “Geraden” (Verbindungslinien) durch die Arbeitsgruppen. Liegt der Punkt auf einer Geraden, dann heißt das, der Mitarbeiter gehört diesem Ausschuss an und nur dann. Dass die Bedingungen erfüllt sind, sehen wir dann daran, dass je zwei Punkte jeweils genau auf einer Geraden liegen und je zwei Geraden genau einen Schnittpunkt besitzen.
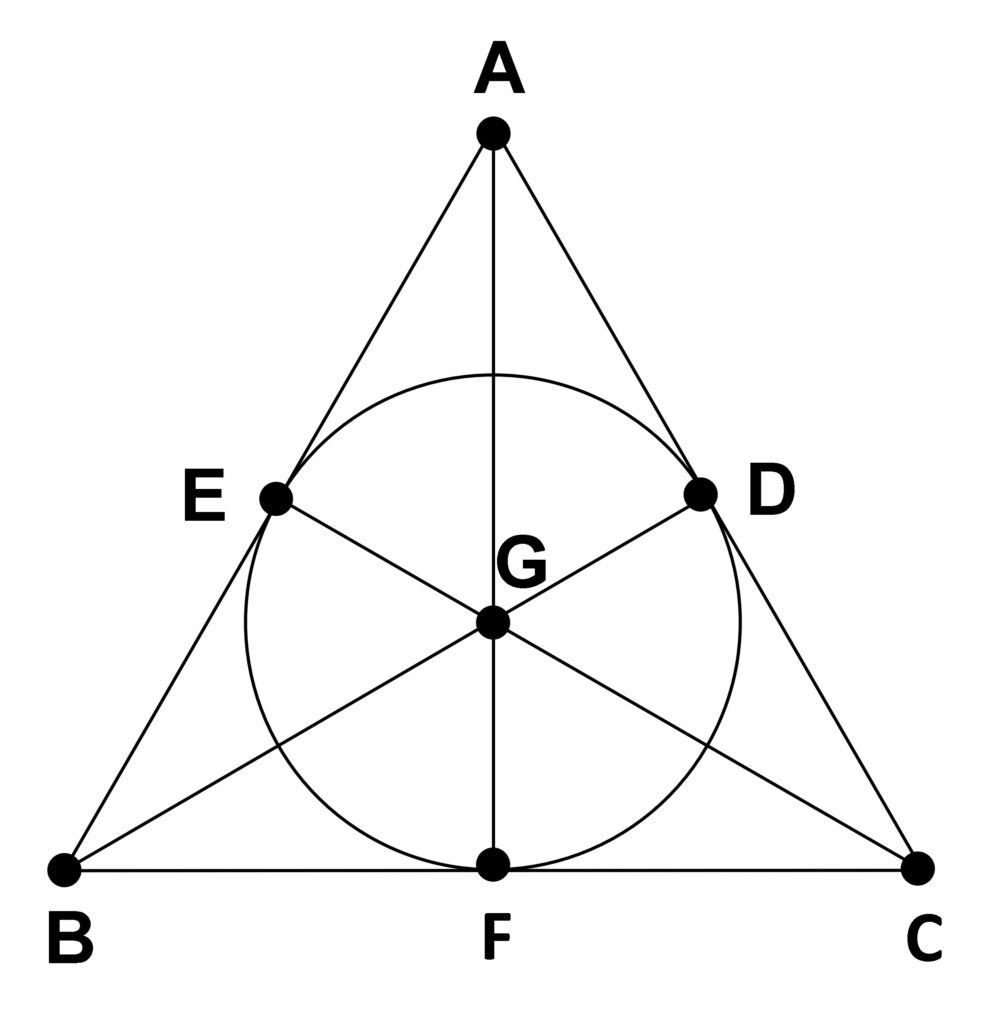
Diese Figur ist in der Mathematik als Veranschaulichung einer Inzidenzstruktur, und zwar der “kleinsten projektiven Ebene” bekannt. Dabei ist diese folgendermaßen definiert. Sie besteht aus der kleinstmöglichen Zahl von Punkten und Geraden, für die gilt:
A1: Je zwei verschiedene Geraden besitzen immer genau einen Schnittpunkt
A2: Je zwei verschiedene Punkte besitzen immer genau eine Verbindungsgerade
A3: Es gibt mindestens vier verschiedene Punkte, von denen nicht drei auf ein und derselben Geraden liegen.
Aus diesen drei Axiomen lässt sich beweisen, dass es für die kleinste solche Struktur genau sieben Punkte und auch sieben Geraden geben muss. Auf jeder Geraden liegen drei verschiedene Punkte und in jedem Punkt schneiden sich drei verschiedene Geraden.
Welche der Axiome, A1, A2 und A3 werden nun von einem Dobblespiel erfüllt?
Dazu betrachten wir die Spiel-Scheiben als die Geraden und die Symbole, die dieselbe Form und Farbe besitzen, als Punkte. Dann gilt: Je zwei verschiedene Geraden (= Spiel-Scheiben) besitzen genau einen Schnittpunkt (=gemeinsames Symbol), d.h. A1 ist erfüllt. Ohne die Gültigkeit von A1 wäre das Spiel im Grunde genommen sinnlos, A1 entspricht der zugrundeliegenden Spielregel, dem Erkennen des einzigen gemeinsamen Symbols zweier Karten. Aber gilt auch, dass je zwei verschiedene Punkte (=verschiedene Symbole) genau auf einer Geraden (=Spiel-Scheibe) liegen, also A2? Dieses Axiom ist nicht erfüllt. Man kann Gegenbeispiele finden. Ohne das Axiom A3 wäre das Spiel völlig uninteressant: Es gäbe nur eine Spielkarte! Das Axiom A2 ist für das Spiel verzichtbar. Allerdings ist jede endliche projektive Ebene als Struktur für ein solches Spiel geeignet. Der Verzicht auf A2 hilft beim Bemühen, mehr Symbole bei weniger Karten verwenden zu können. Zu wenige Symbole machen das Erkennen gleicher Symbole zu leicht und zu viele Karten machen das Spiel zu unhandlich. Gedanklich lässt sich daher folgender Kompromiss rechtfertigen: Man verzichtet auf das Axiom A2, indem man auf eine Anzahl Karten verzichtet, also keine endliche projektive Ebene benutzt, sondern nur eine endliche Inzidenzstruktur ohne die Gültigkeit von A2. Für das konkrete Spiel bedeutet das, es gibt mindestens zwei verschiedene Symbole (Punkte), die nicht genau auf einer Karte (Geraden) liegen.
Wie das Weglassen von Karten erfolgen kann, ohne das Spiel zu stören, dazu kehren wir noch einmal zum Beispiel des Objektes mit den sieben Ringen zurück. Nehmen wir als Beispiel den Ring mit den Buchstaben DEF weg:
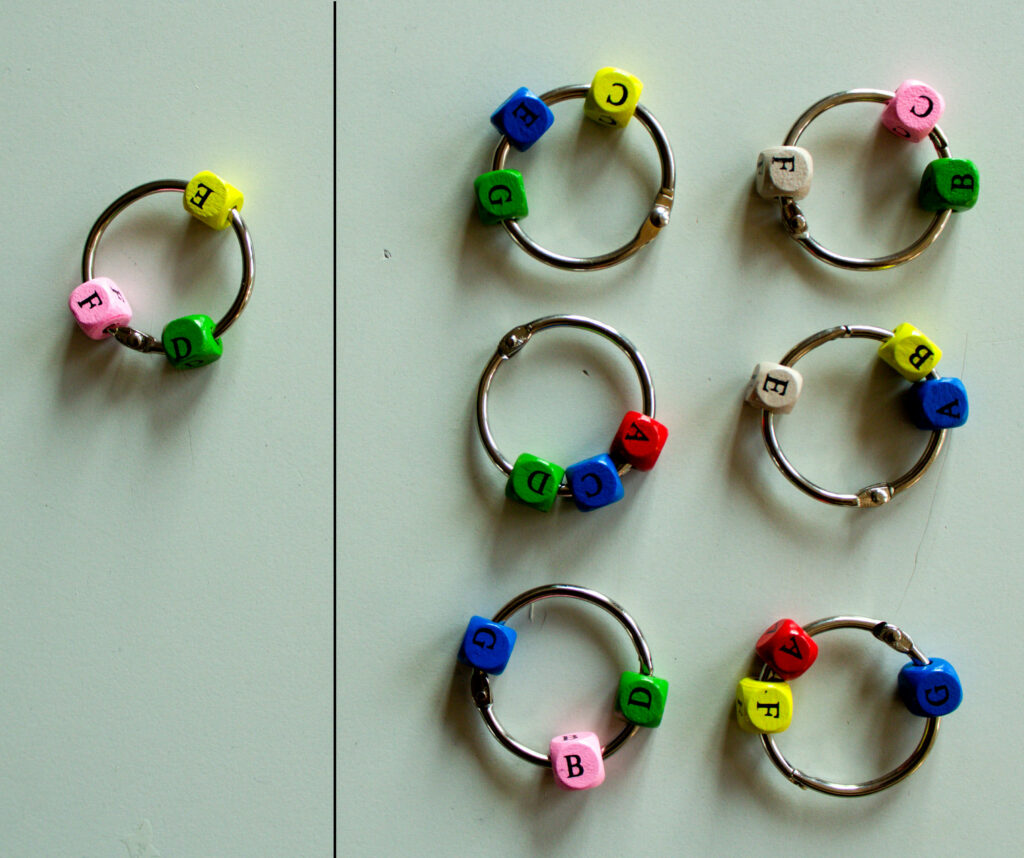
Dann gilt zwar weiter, dass je zwei der restlichen sechs Ringe genau einen der sieben Buchstaben gemeinsam haben (A1) und es mindestens vier Buchstaben gibt, die sich nicht auf einem Ring befinden (A3). Aber es gibt jetzt mindestens zwei verschiedene Buchstaben, die sich nicht auf einem gemeinsamem Ring befinden, z.B. D und E (oder D und F oder E und F). Man kann auch mehr als einen Ring herausnehmen, und zwar mit der gleichen Argumentation, aber wegen A3 müssen wenigstens zwei Ringe mit mindestens vier verschiedenen Buchstaben bleiben. Hier das Beispiel, bei dem zwei Ringe herausgenommen wurden:
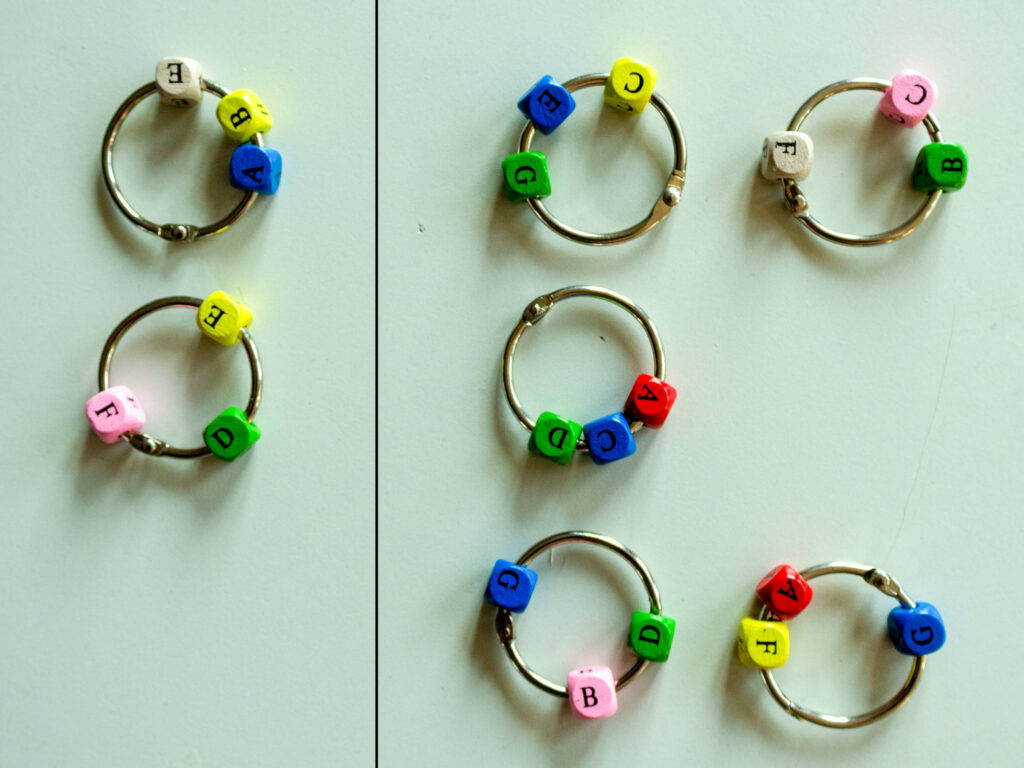
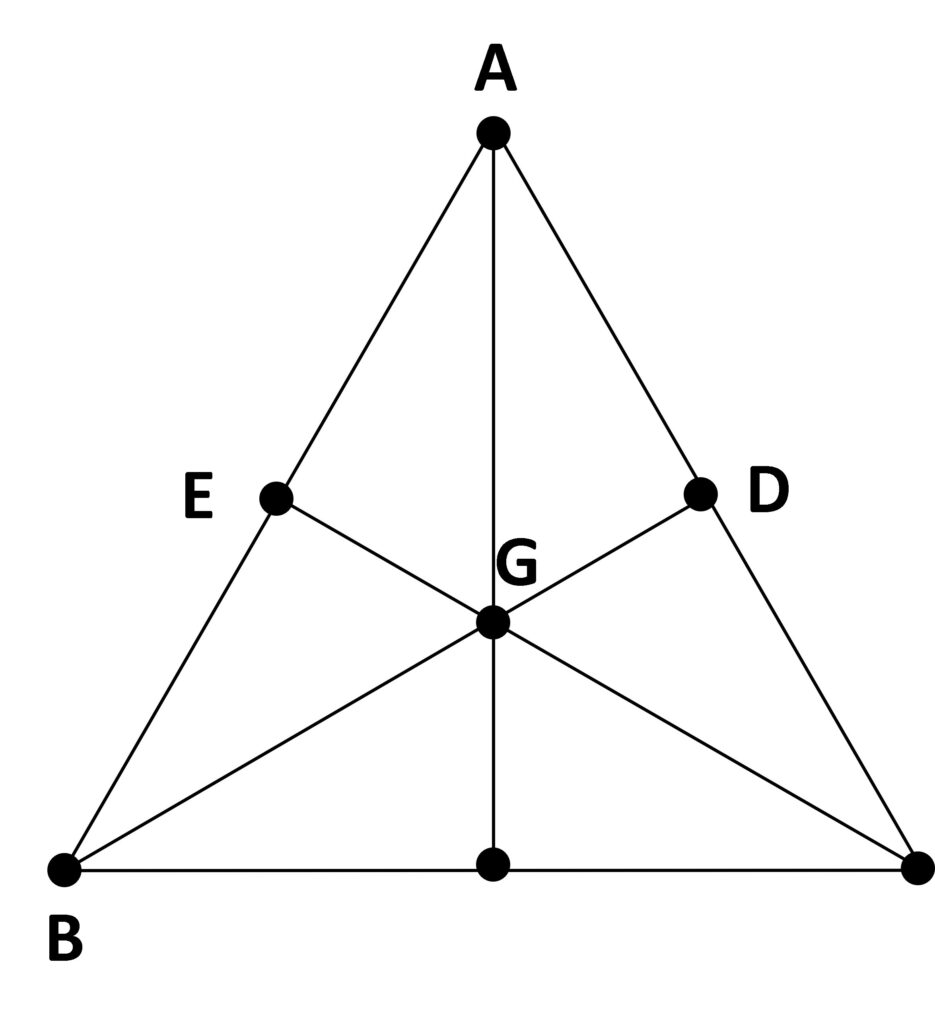
Bezogen auf die grafische Darstellung der kleinsten projektiven Ebene stellt sich die Herausnahme der Geraden DEF bzw. der beiden Geraden DEF und ABE so dar:
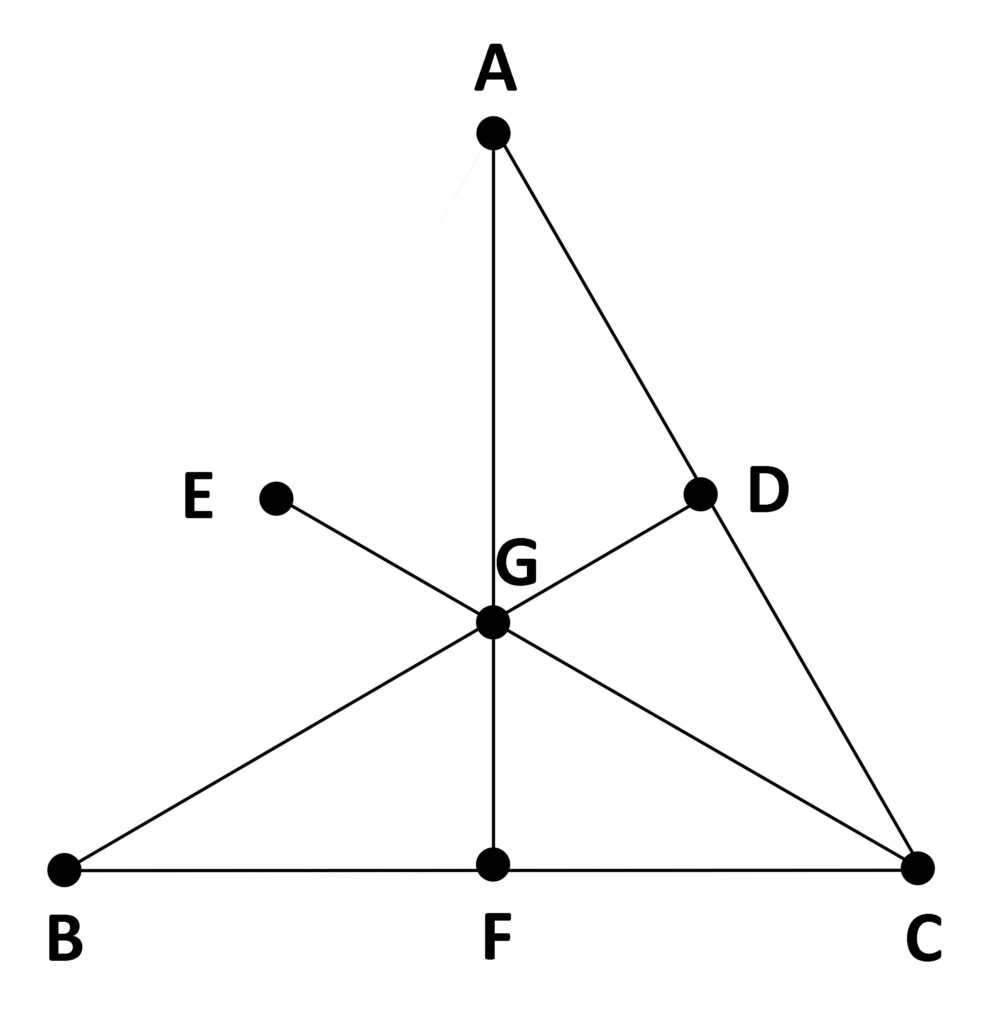
Bei einem Dobble-Spiel, das sich auf die kleinste projektive Ebene bezöge, müssten auf jeder Scheibe drei Symbole sein. Man könnte es ohne weiteres mit den Ringen (oder Kärtchen) spielen, wäre aber als Spiel wohl doch zu langweilig. Das in der Mathothek verfügbare Dobble-Spiel hat auf jeder Scheibe sechs verschiedene Symbole und leitet sich daher von der projektiven Ebene der 5. Ordnung her. Besonders beliebt ist das Dobble-Spiel mit acht Symbolen auf jeder Scheibe und damit der projektiven Ebenen 7. Ordnung im Hintergrund.
Projektive Ebenen haben viele angenehme Eigenschaften, die sich aus der Symmetrie von Punkten und Geraden ergeben, genauer gesagt aus der Dualität von Punkt und Gerade. Jede wahre Aussage wird wieder zu einer wahren Aussage, wenn man Punkt und Gerade vertauscht sowie verbinden und schneiden. Es gibt nicht den Sonderfall, dass zwei Geraden auch keinen Punkt gemeinsam haben können, also parallel sind.
Von unserer vertrauten euklidischen Geometrie sind wir gewohnt, dass es zwar zu je zwei verschiedenen Punkten eine Verbindungsgerade gibt, aber nicht immer gibt es zu zwei verschiedenen Geraden einen Schnittpunkt, die Geraden nennen wir dann parallel.
Die kleinste affine Ebene ist dann axiomatisch folgendermaßen beschrieben:
A1: Je zwei verschiedene Punkte besitzen genau eine Verbindungsgerade.
A2: Es gibt zu jeder Geraden und jedem nicht auf dieser Geraden liegendem Punkt genau eine Gerade, die keinen gemeinsamen Punkt mit der ersten Geraden hat. (Parallelenpostulat).
A3: Es gibt mindestens drei verschiedene Punkte, die nicht auf derselben Geraden liegen.
Die kleinste affine Ebene lässt sich so veranschaulichen:
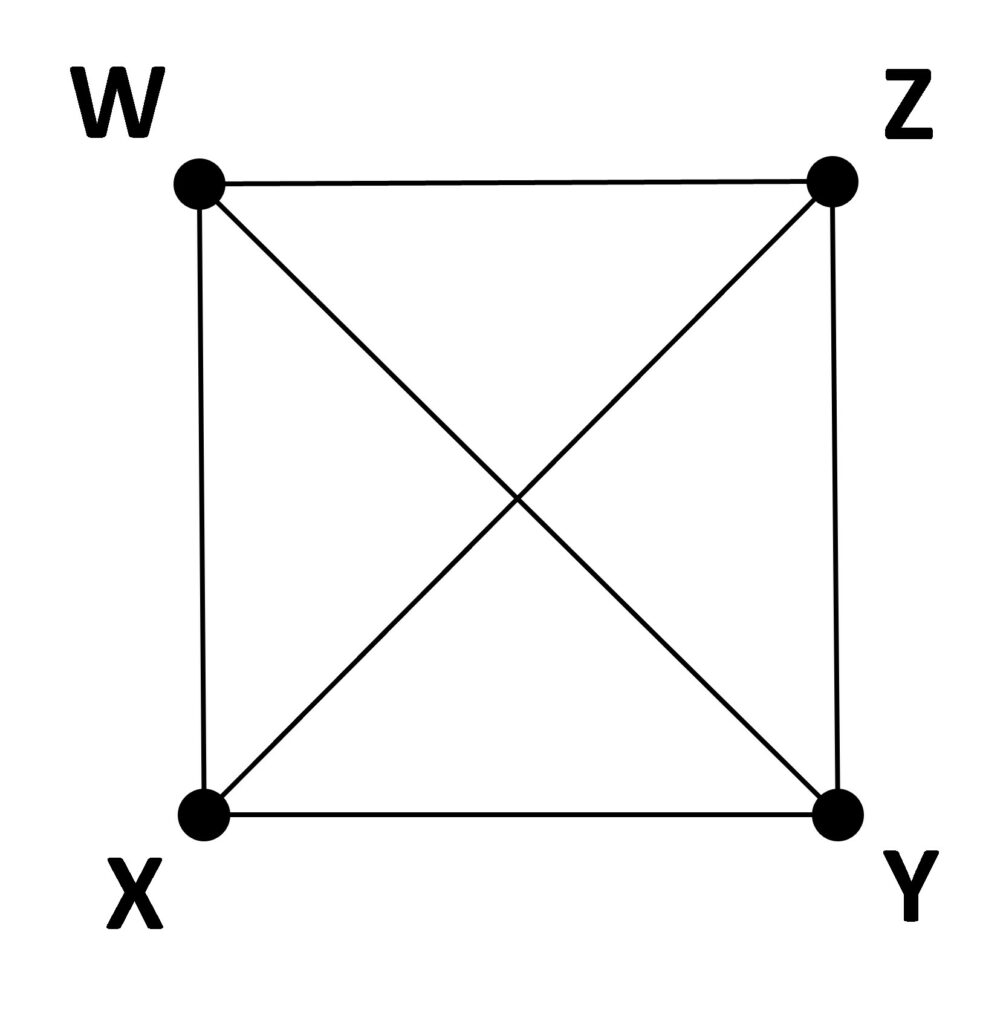
Sie besitzt vier verschiedene Punkte und sechs verschiedene Geraden. Dabei gibt es drei Geradenpaare, die jeweils keinen gemeinsamen Schnittpunkt besitzen. Neben den Geraden durch X, Y und W, Z sowie W, X und Z, Y sind auch die beiden Geraden X, Z und W, Y parallel, d.h. besitzen keinen gemeinsamen Punkt.
Für unsere Arbeitsgruppenbildung bzw. unser Ringspiel würde das bedeuten: Sollten aus vier Personen sechs Teams aus je zwei Personen gebildet werden, so würde die gewünschte Vernetzung nicht machbar sein.
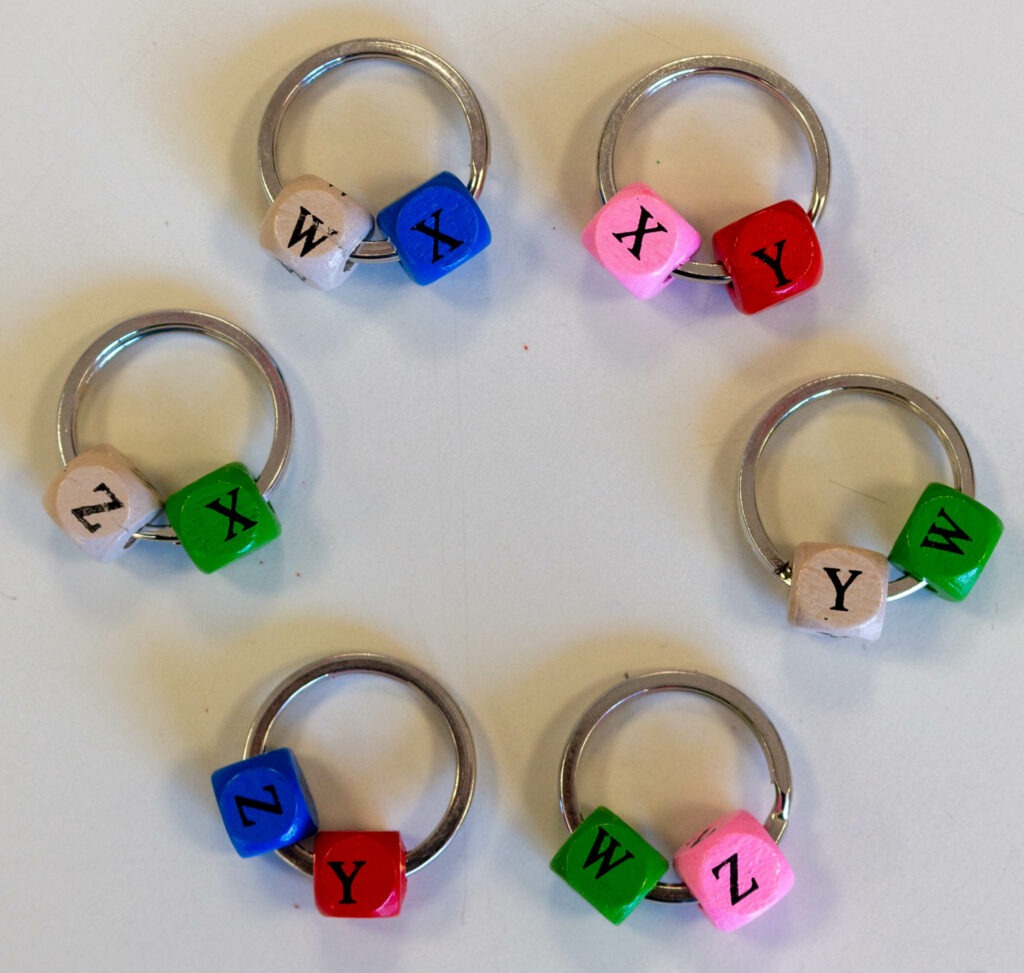
So kann das Spiel Dobble mit den in der Mathothek zugehörigen Objekten ein Zugang zur abstrakten oder axiomatischen Mathematik werden, wo erkennbar wird, dass es nur auf die Mengen mit ihren Elementen und die definierten Beziehungen zwischen ihnen ankommt, ob es sich dann bei den Modellen um Buchstaben auf runden Karten oder Ringen mit würfelförmigen Körpern oder Kärtchen mit Namen handelt, ist dabei egal. Namen “sind Schall und Rauch”, auf die Beziehungen kommt es an.

“Mathephobiker” könnten immerhin den ganzen Ausführungen entnehmen, dass sie das Spiel auch dann weiter ohne Probleme benutzen können, wenn die eine oder andere Karte verloren geht, mindestens jedoch solange noch mehr als eine Karte vorhanden ist. A3!