Wie können wir helfen?
Da staunten hier schon ganz andere Besucher: Was hat eine solche Holztruhe mit dieser Fülle an Stoffmustern in der Mathothek zu suchen? Was haben denn die vielen mehr oder weniger eleganten bunten Muster mit der nüchternen Mathematik zu tun?
Nun, die Mathematik hat sich seit der griechischen Antike, für die Mathematik im Wesentlichen Geometrie war, immer schon mit Mustern auseinandergesetzt. Muster fordern den Geist des Menschen heraus, Strukturen zu suchen, Regelmäßigkeiten zu entdecken, Gesetze zu erkennen und zu formulieren. Wer sich auf die Truhe mit ihren Ministoffballen einlässt, wird spüren, dass dieses Anliegen in jedem Menschen vorhanden ist und jeden zu faszinieren imstande ist.
Regelmäßige Muster in der Ebene entstehen durch Translationen (= Verschiebungen) eines Ausgangsmotivs (= Rapport) in zwei nicht parallelen Richtungen. Mathematisch spricht man von einer Zelle oder einem Grundparallelogramm, das durch die beiden Verschiebungsstreifen entsteht. Es gibt dann weiter die Möglichkeit, aufgrund zusätzlicher Symmetrieeigenschaften jedes Muster in eine der mathematisch möglichen 17 Symmetriegruppen (=Symmetrietypen) einzuordnen.
Bei ebenen Ornamenten gibt es außer der immer vorhandenen Translation noch die weiteren Symmetrieabbildungen Achsenspiegelung, Gleitspiegelung, Drehung um 180° (=Punktspiegelung), Drehung um 90° bzw. 270°, Drehung um 120°, bzw. 240° und die Drehung um 60° bzw. 300°.
Falls ein Muster – ein ebenes Ornament – durch eine solche Abbildung auf sich abgebildet wird, so sagen wir, dass das Muster die entsprechende Symmetrie besitzt (Punktspiegelung – punktsymmetrisch).
Die verschiedenen Symmetrieabbildungen können nun nicht in jeder beliebigen Kombination auftreten. So zieht eine Achsenspiegelung mit waagrechter Spiegelachse und eine Achsenspiegelung mit senkrechter Spiegelachse mathematisch notwendig eine Punktspiegelung am Schnittpunkt der Achsen nach sich. Diejenigen Symmetrieabbildungen, die sich kombinieren lassen, bilden die mathematische Struktur einer Gruppe.
Dieser Begriff ist in der Mathematik besonders grundlegend und verbreitet. Eine Gruppe ist eine bestimmte Menge von Elementen mit einer Verknüpfung. Hier besteht die Gruppe aus einer Menge von Symmetrieabbildungen und der Hintereinanderausführung als Verknüpfung. Damit es sich wirklich um eine Gruppe handelt, müssen dann bestimmte Gesetze erfüllt sein. So müssen u.a. alle Verknüpfungen von zwei beliebigen Elementen wieder zur Menge gehören, oder zu jedem Element muss es ein Umkehrelement geben. In unserem Fall bedeutet das: Werden zwei Abbildungen aus einer Symmetriegruppe hintereinander ausgeführt, so muss auch hier das Muster wieder auf sich abgebildet werden, jede Achsen- und jede Punktspiegelung ist gleich ihrer Umkehrabbildung, die Drehung um 120° hat als Umkehrfunktion die Drehung um 240° usw. Dazu muss es in jeder Gruppe ein neutrales Element geben, d.h. in unserem Fall ist das die Drehung um 360° (= identische Abbildung).
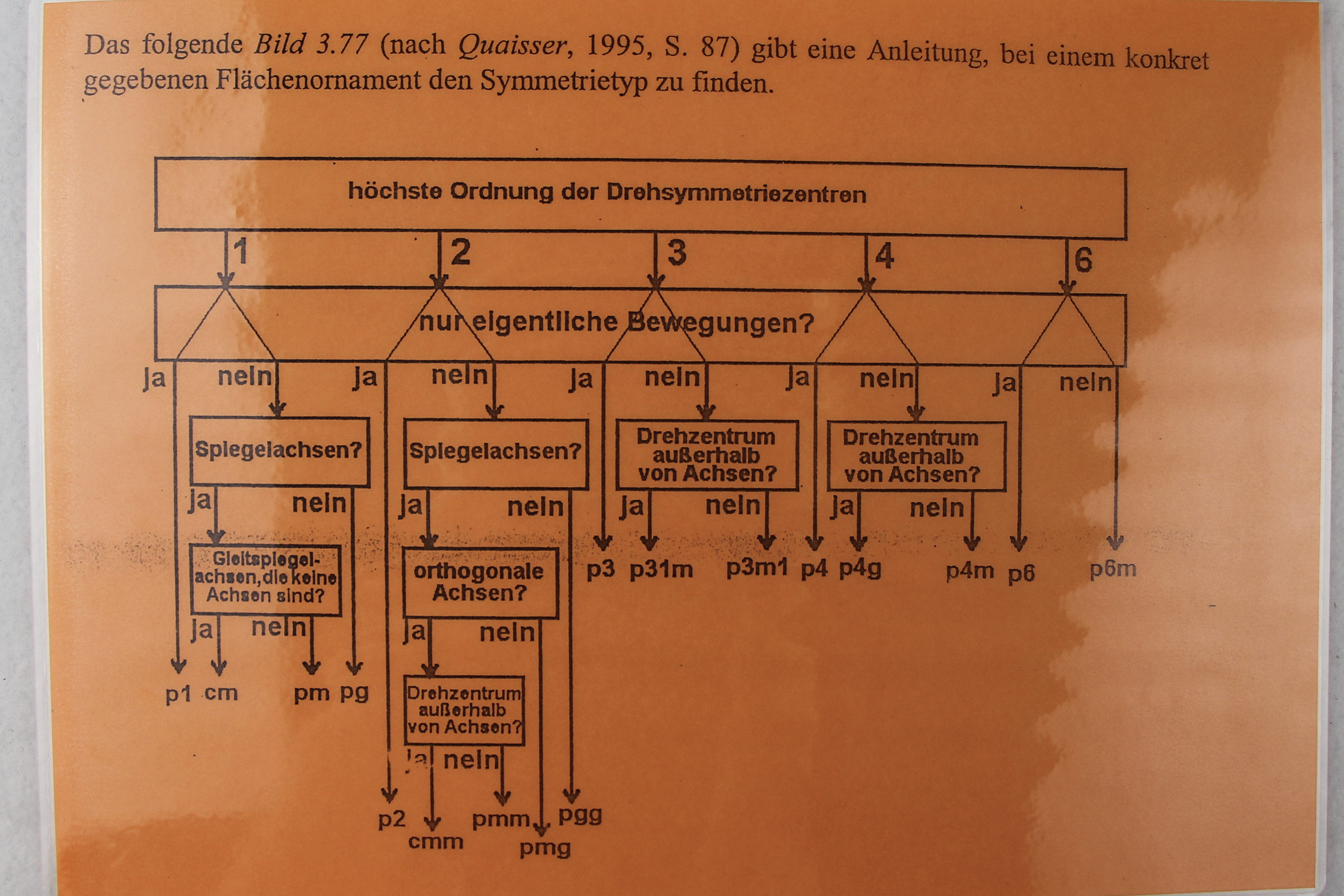
In der “Übersicht über die Symmetrietypen” (nach Brettschneider, 1978) sind die 17 Typen vollständig erklärt und anschaulich dargestellt. Die vierspaltigen kristallographischen Bezeichnungen der 17 Symmetrietypen sind ebenfalls beschrieben. Darüber hinaus gibt es eine sehr gute Anleitung (nach Quaisser, 1995), um bei einem konkret vorliegenden Flächenornament den Symmetrietyp schrittweise zu finden. Der erste Schritt ist dabei die Feststellung von Drehsymmetrien zur Bestimmung der “höchsten Ordnung der Drehsymmetriezentren”, d.h. man untersucht das Muster auf Drehsymmetrie (= eigentliche Bewegungen). Gibt es nur die Drehung um 360°, dann beträgt die höchste Ordnung des Drehzentrums 1. Die größte Drehzentrumsordnung ist 6, das entspricht den Drehungen um 60°, 120°. 180°, 240°, 300° und 360°. (Zwei laminierte Blätter)
Die vier Symmetrietypen mit 1 als höchster Ordnung der Drehsymmetriezentren:
Die fünf Symmetrietypen mit 2 als höchster Ordnung der Drehsymmetriezentren:
Die drei Symmetrietypen mit 3 als höchster Ordnung der Drehsymmetriezentren:
Eine originale Stoffprobe des Symmetrietyps p3m1 war nicht aufzutreiben. Deswegen gibt es ersatzweise ein manipuliertes (links) und ein aus Geschenkpapier bestehendes Beispiel (rechts).
Die drei Symmetrietypen mit 4 als höchster Ordnung der Drehsymmetriezentren:
Die zwei Symmetrietypen mit 6 als höchster Ordnung der Drehsymmetriezentren:
Natürlich ist dieses Thema in keinem Lehrplan für Mathematik vorgesehen. Trotzdem ist es ein wundervolles Stück Mathematik: Es findet Anwendungen in den Naturwissenschaften, in der Kunst, der Kunsttheorie und in der Mathematik bei dem großen Thema der Untersuchungen von Mustern und Strukturen. Es schafft Ordnung, Einsicht und Übersicht in einem zunächst völlig unübersichtlichen Bereich, dessen überwältigende Fülle einen zu erschlagen droht. Der Gegenstand selbst ist nicht unbedingt lebensnotwendig, aber entspricht einem Urbedürfnis des Menschen zu allen Zeiten nach Schönheit und Kultur. Es kann sogar zum Vergnügen werden, während einer Busfahrt oder einem langweiligen Vortrag das Muster des Hemdes eines Nachbarn oder des Kleides einer Nachbarin mal eben zu analysieren. Natürlich lassen sich auch Tapetenmuster unter diesen Gesichtspunkten anschauen. Ganz zu schweigen von der Faszination einer solchen Untersuchung islamischer Ornamente.
In der Stoffkiste liegen unter den Ministoffballen eine Anzahl Stoffmuster, die zur Analyse und Zuordnung herausfordern. Viel Spaß!
Gerade im Alltag und in scheinbar unübersichtlichen Bereichen Mathematik aufzuzeigen, ist ein wesentlicher Weg der Mathothek.