Wie können wir helfen?
Ein Geobrett ist ein Brett aus Holz, in das Nägel nicht vollständig eingeschlagen wurden, sodass man noch Fäden oder Gummiringe an ihnen befestigen kann. Die Nägel stehen in Reihen und Spalten, sodass ein gleichmäßiges Raster aus gleich großen Quadraten entsteht.
Mit den bunten Gummiringen lassen sich die verschiedensten gradlinig begrenzten Vielecke (=Polygone) erzeugen. Nimmt man an, dass die Nägel waagrecht bzw. senkrecht jeweils 1cm voneinander entfernt sind, so liefert der Satz von Pick einen einfachen Weg zum Ergebnis:
- Man bestimmt zunächst die Anzahl der Grenzpunkte g
- Dann bestimmt man die Anzahl der inneren Punkte i
Den Flächeninhalt A des Gitterpolygons berechnet man dann nach der einfachen Formel:
A=g:2+i-1
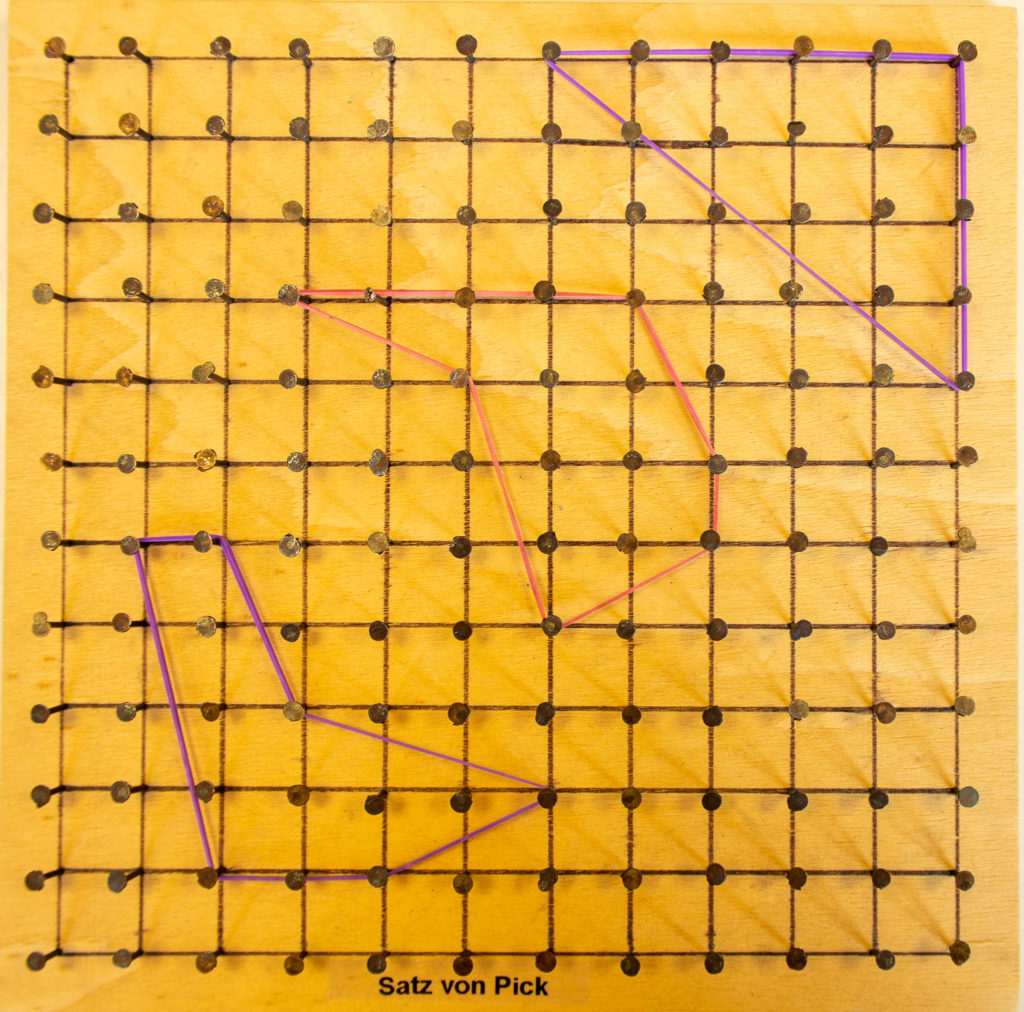
Berechne auf diesem Wege die Flächeninhalte der folgenden drei Polygone. Multipliziert man die drei Ergebnisse, so erhält man 847,875.
Drei weitere Beispiele:
Die Lösung für das letzte Beispiel: g=17, i=19, dann ist der Flächeninhalt mit dem Satz von Pick A=20:2+19-1=28.
In der Mathothek sind die beiden am häufigsten gestellten und am meisten erwünschten Fragen:
- Ist das immer so?
- Warum ist das immer so?
Versuche, die beiden Fragen selbständig zu beantworten. Zerlege jedes solches Pick’sche Polygon in Quadrate und rechtwinklige Dreiecke zu zerlegen.
Warum geht das immer?
Kannst Du jetzt die Formel von Pick bestätigen?