Wie können wir helfen?
Es handelt sich bei diesen drei Exponaten der Mathothek um eine Herausforderung an unser analytisches und logisches Denken. Dieser Weg führt in allen drei Fällen zu erstaunlich einfachen und eleganten Antworten auf die jeweils gestellten Fragen.

Das bekannteste der drei Probleme ist das “verstümmelte Schachbrett”. Ausgangspunkt ist ein ganz normales Schachbrett. Von diesem Schachbrett sind an zwei Ecken je ein dunkles Feld entfernt worden. Die Frage, die beantwortet werden soll, lautet nun: “Lassen sich die verbliebenen Felder des verstümmelten Schachbretts mit Dominosteinen oder den bunten Doppelquadraten unseres Exponats vollständig, d.h. lückenlos und ohne Überlappung, bedecken?”
Erster Versuch:

Ergebnis: Es bleiben zwei weiße Felder leer. Man wird wahrscheinlich weitere Versuche mit zusätzlichen Überlegungen starten und scheitern.
Erst die Überlegung, dass zwei dunkle quadratische Felder entfernt wurden und damit zwei helle Felder mehr als dunkle vorhanden sind und da auf keinem Schachbrett zwei helle Felder nebeneinander liegen und somit die beiden verbliebenen hellen Quadrate durch kein Doppelquadrat abgedeckt werden können, zeigt, dass das Problem unlösbar ist.
Dass für die Lösbarkeit oder Unlösbarkeit die Färbung der Doppelquadrate keine Rolle spielt, sieht man an einer Variante des Objekts, bei der die Doppelquadrate aus Spiegelfolie bestehen.

Zu dem zweiten Exponat gehört eine hölzerne Grundplatte mit einem Raster aus 10×10 Quadraten. In der ersten Zeile enthält jedes der zehn Quadrate die Zahl 1, in der zweiten die Zahl 5, in der dritten wieder die 1, in der vierten wieder die 5 usw. Dazu gibt es noch blaue transparente Plättchen in L-Form, mit denen sich je vier zusammenhängende Quadrate abdecken lassen.

Die zu beantwortende Frage lautet diese Mal: “Kann man das Quadrat mit 25 blauen Plättchen vollständig und ohne Überlappung bedecken? “Hier der erste Versuch einer Lösung der Aufgabe. Es bleiben vier Quadrate übrig, die nicht der Regel gemäß abzudecken sind.
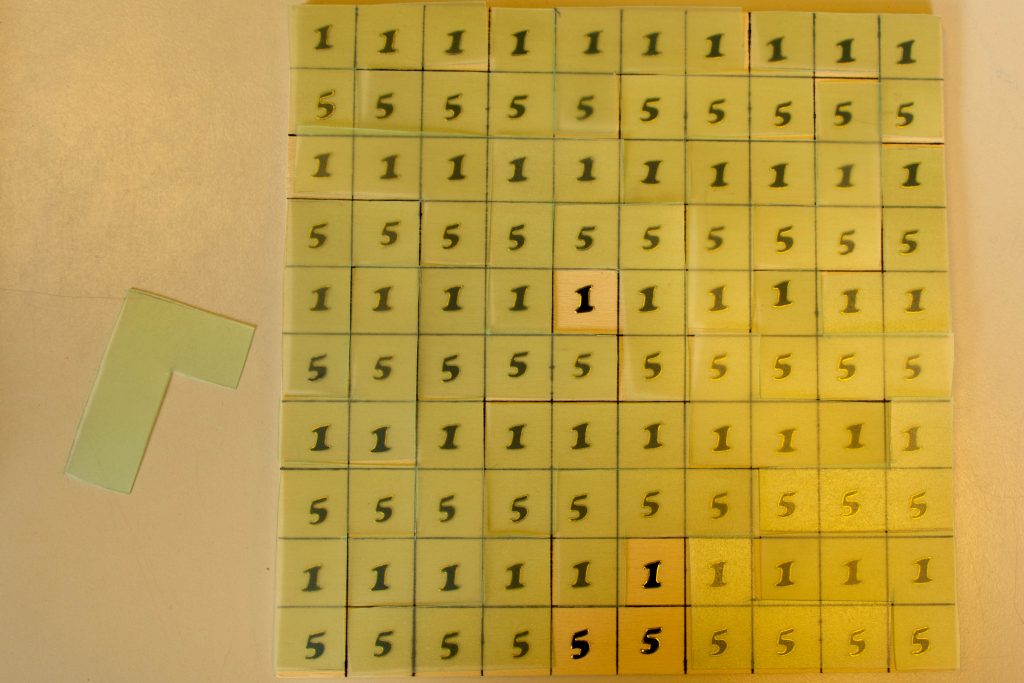
Einige Versuche, die Aufgabe konkret zu lösen, scheitern. Nach mehreren Frusterlebnissen stellt sich die Frage, ob diese Aufgabe überhaupt zu lösen ist. Aber der Frust und die – ganz egal wie vielen – Gegenbeispiele sind kein mathematischer Beweis für die Unlösbarkeit der Aufgabe.
Natürlich haben die Zahlen auf dem Brett nicht nur eine dekorative Funktion. Sie liefern den Ansatz für einen Beweis: Addiert man alle Zahlen auf dem Brett, so erhält man 5·50+5·10=300. Mit einem der Plättchen lässt sich entweder die Summe 8 oder die Summe 16 abdecken. Angenommen, das Quadrat ließe sich vollständig abdecken, dann müsste die Summe aller Zahlen auf dem Brett durch 8 teilbar sein. Das ist ein Widerspruch. 300 lässt sich nämlich nicht durch 8 teilen. Also ist die Annahme, dass sich das Quadrat vollständig und überlappungsfrei bedecken lässt, falsch. Folglich ist bewiesen, dass die gestellte Aufgabe unlösbar ist.
Da hier eine als notwendig erkannte Bedingung, (Die Gesamtsumme von 300 ist ist durch 8 teilbar) nicht erfüllt ist, muss die Behauptung (Es gibt eine entsprechende Belegung des Bretts.) falsch sein, und damit ist bewiesen, dass diese Aufgabe unlösbar ist.
Es gibt noch ein weiteres ähnliches Exponat. Aus dem Grundbrett des vierten Exponats und den aus je vier gleichen Holzwürfelchen zusammengeklebten T-Formen soll ebenfalls die Frage nach der Abdeckung geklärt werden. Erste Überlegung, dass 100 durch 4 teilbar ist, macht Mut. Jedoch Versuch für Versuch scheitert. Wie finden wir auf rein logischem Weg die Lösung? Die Einsen und Fünfer haben wohl auch hier keinen rein dekorativen Zweck. Welche notwendige Bedingung ist hier verletzt?
Viel Spaß!

