Wie können wir helfen?

Eine gläserne Blumenvase – einfach, schnörkellos, zweckdienlich. Sie ist mit einer roten Flüssigkeit gefüllt, um ihre Eleganz noch hervorzuheben. Sie ist zweckdienlich, weil ihre Form dem meist verwendeten Prinzip der Floristen, einen Strauß zu binden, perfekt entspricht.
Beide sind mathematisch gesehen, einschalige Hyperboloide – natürlich nur mehr, die Vase, oder weniger gut angenähert, der Strauß. Der Name kommt von dem entsprechenden Kegelschnitt: der Hyperbel.

Um ein einschaliges Hyperboloid zu erhalten, lässt man eine Hyperbel um die waagrechte Achse, die Symmetrieachse der beiden Hyperbeläste rotieren. Lässt man die Hyperbel um die andere Symmetrieachse rotieren, so entstehen zwei getrennte symmetrische Körper ein zweischaliges Hyperboloid. In der Architektur sehen wir das einschalige Hyperboloid z.B..in der Gestalt der Kühltürme. Aber auch die “Bettelobjekte” vieler Museen haben die Form eines solchen einschaligen Paraboloides. Diese sind große Potenzialtrichter, die meist im Eingangsbereich stehen und in die man gültige Münzen hineinrollen lassen kann. Diese Münzen rollen dann in langsam kleiner werdenden Spiralbögen in einen Sammelbehälter, um als Spenden zu dienen.


Dieser kleine Potenzialtrichter in der Mathothek hat auch die Gestalt eines einschaligen Hyperboloids und stammt aus dem Museumsshop des Mathematikums in Gießen. In der Mathothek stehen allerdings Münzen aus der DM-Zeit für Experimente zur Verfügung.
Schon bei dem “Floristen-Hyperboloid” entsteht die Form durch die spezielle Anordnung der relativ geraden Blumenstiele, sie werden nicht parallel zur Achse des Straußes angelegt, sondern windschief. Dieser Hocker aus einem “Eine Welt Laden” zeigt den Zusammenhang von Hyperboloid und Geraden noch deutlicher:
Dieses interessante Sitzmöbel besteht aus Bambus und ist sehr stabil. Man sieht, dass die Stäbe ähnlich wie bei dem Blumenstrauß angeordnet sind. Die besondere Stabilität des Hockers wird dadurch erreicht, dass im Inneren eine zweite Reihe von Bambusstäben gegenläufig angeordnet ist.
Ein weiteres Exponat der Mathothek zeigt den Zusammenhang von Geraden, die in einem Hyperboloid enthalten sind: Es handelt sich dabei um zwei hölzerne Kreisscheiben, die drehbar in der Mitte durch eine Achse verbunden sind. Am Rand des Kreises sind rote Gummifäden senkrecht zwischen den Kreisen gespannt. Sie stellen die im Hyperboloid enthalten Geraden dar. Denn da es Gummifäden sind, bildet jeder von ihnen eine Gerade, und zwar solange sie gespannt sind. Das einschalige Hyperboloid lässt sich folglich durch eine Gerade erzeugen. Dazu muss eine Gerade nur um eine Achse rotieren. Falls diese beiden Geraden – Achse und rotierende Gerade – parallel sind, entsteht ein Zylinder und falls sie sich schneiden, so entsteht ein Doppelkegel. Nur wenn die beiden Geraden weder das eine noch das andere sind, also windschief sind, dann entsteht bei der Rotation ein Hyperboloid.

Wenn man nun dieses Objekt in die Hände nimmt und die beiden blauen Grundflächen gegeneinander dreht, so wandelt es sich von einem Zylinder über immer “schlankere” Hyperboloide zu einem Doppelkegel.
Natürlich lässt sich der Zylinder in beide Richtungen drehen. Es gibt auch noch ein nicht drehbares Fadenmodell mit zwei verschiedenen Hyperboloiden:
In der Mathothek gibt es noch einige Dinge, die ein einschaliges Hyperboloid als Vorbild haben.
Was passiert aber, wenn die Kreise immer größer und größer werden, wenn wir für dieses Experiment zwei Geraden nehmen? In der Mathothek gibt es ein weiteres Exponat, dass aus zwei Holzleisten besteht, die analog zu den beiden Kreisen mit schwarzen Gummifäden bespannt sind.
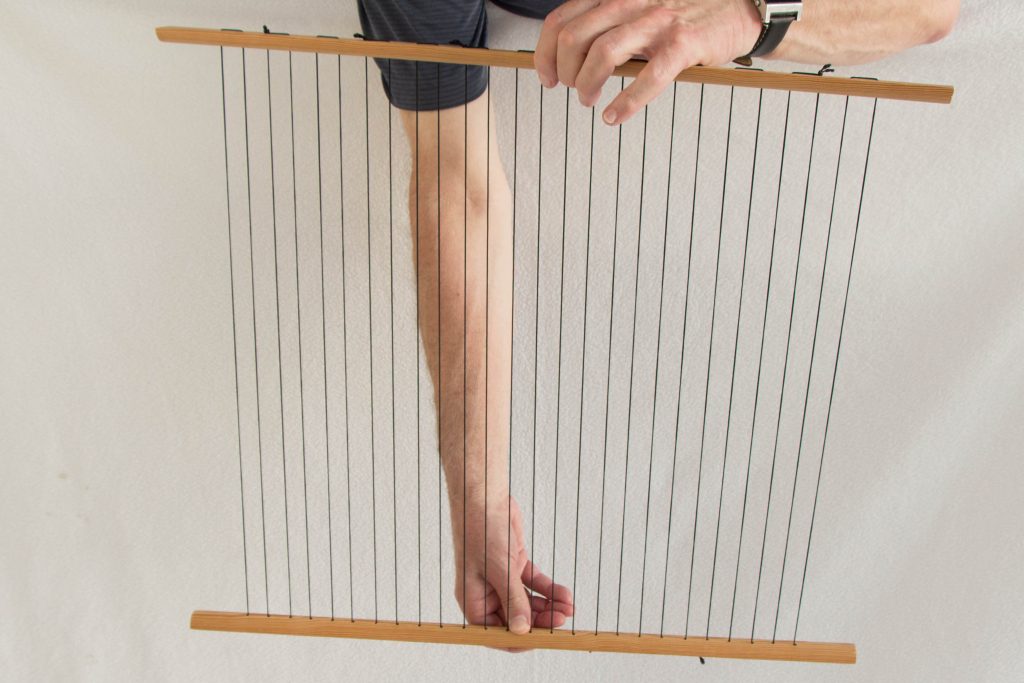
Die beiden Holzstäbe, oben noch parallel gehalten werden, werden nun windschief so verdreht, dass die Gummifäden aber immer gespannt bleiben.
Was man jetzt beobachtet ist natürlich vergleichbar zu den Drehungen der Kreise. Zunächst haben wir eine Ebene, die mit jeder Geraden auch alle ihre Parallelen enthält. Durch das Drehen werden dann nach und nach mehr oder weniger gekrümmte Flächen daraus. Die gespannten Gummifäden zeigen, dass die gekrümmte Fläche weiter von unendlich vielen Geraden durchzogen wird. Aber die beiden Holzstäbe stehen auch für Geraden, die in dieser gekrümmte Ebene enthalten sind. Es gibt schließlich eine Situation, in der sich alle Geraden in einem Punkt zu schneiden scheinen, der durch unseren Sehstrahl entsteht.
Das Besondere und Charakteristische an den beiden Strukturen – Hyperboloid und krümmbare Fläche – ist es, dass sie jeweils zwei verschiedene Mengen von Geraden enthalten.
Eine Fläche auf einer Kugel ist auch eine gekrümmte Fläche. Aber wie groß die Kugel auch immer ist, sie kann keine Geraden enthalten. Eine Gerade und eine Kugeloberfläche können immer nur höchstens zwei gemeinsame Punkte besitzen. Im Falle von einem gemeinsamen Punkt handelt es sich um eine Tangente.
Aber es gibt noch unendlich viele gekrümmte Flächen, in der nur eine Menge von Geraden liegt. In Mainz gibt es vor dem Rathaus eine Skulptur, die aus vielen Metallstäben besteht:

Diese Skulptur “Lebenskraft” von dem spanischen Künstler Andreu Alfaro (1929 – 2012) zeigt uns, welche vielfältige Fläche mit einer Geraden erzeugt werden kann. Jedes Mal, wenn man eine Gerade durch den Raum bewegt, erzeugt man eine solche Regelfläche. Bei einer Regelfläche geht durch jeden Punkt dieser Fläche eine Gerade, die ganz in ihr liegt. Die Skulptur ist aus Aluminium und entstand 1979. In Mainz wurde sie 1982 vor dem Rathaus aufgestellt.
Auch eine klassische Zahnpastatube ist im Prinzip eine Regelfläche, wenn man sich den Öffnungsbereich wegdenkt. Die untere Begrenzung des Zahnpasta-Behälters ist ein Kreis, die die untere eine gerade Strecke und die “Gräten”, also die in der Regelfläche steckenden Geraden verbinden Kreis- und Streckenpunkte.
Der unten gezeigte Christbaumschmuck besteht aus kleinen zusammengesetzten “Regelflächenstückchen”:






















