Wie können wir helfen?
Wie das Binärsystem (=Dualsystem=Zweiersystem) funktioniert, wird in dem Artikel “Binär-, Dual- oder Zweiersystem – Was der Stinkefinger wirklich bedeutet” erklärt. Hier geht es um einige andere Verwendungen des Binärsystems, z.B. in dem folgenden Trickspiel – Zahlenraten im Binärsystem:

In einem kleinen Metallkästchen befinden sich sechs gelbe Karten mit schwarzen Zahlen. Die Verteilung der Zahlen, die im Dezimalsystem geschrieben sind, erscheint zunächst völlig chaotisch. Allerdings fällt auf, dass keine Zahl größer als 63 ist. Stellen wir uns nun den Ablauf eines Spiels vor: A ist der Ahnungslose und E ist der Eingeweihte.
E: “Wähle eine Zahl zwischen 1 und 63 (einschließlich) und schreibe sie auf einen Zettel, ohne dass ich sie sehen kann.”
A: “Ich bin fertig.”
E: “Ich lege dir jetzt alle Karten hin. Du legst alle Karten zur Seite, auf denen sich deine Zahl befindet.”

A schaut sich die Karten genau an und legt vier Karten extra.
A: “Fertig! Meine Zahl befindet sich nur auf den unteren vier Karten.”
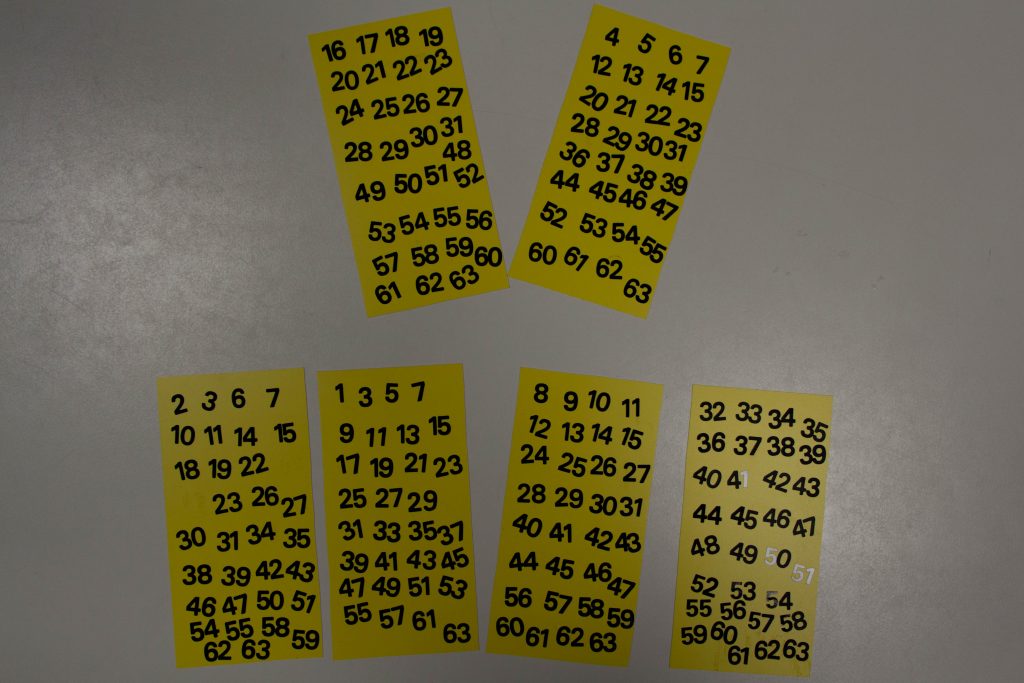
E: “Es ist die 43.”
A: “Toll! Stimmt!”
Natürlich möchte A nicht ahnungslos bleiben und dumm sterben. Also fragt er E.
E: “Da du ja Mathe uncool findest, erkläre ich dir nur den Trick. Ich habe bloß die Zahlen, die oben in der linken Ecke deiner Karten stehen, addiert. Also 2+1+8+32=43!”
Ob der Wissensdurst von A damit gestillt war, oder ob er den Trick doch auch mathematisch verstehen wollte – wie die Besucherinnen und Besucher der Mathothek -, weiß ich nicht.
Du kannst nun versuchen, das Geheimnis selbst zu lüften oder es Dir erklären lassen.
Wenn wir uns die sechs Karten ansehen, dann stellen wir fest, dass in der oberen linken Ecke jeder Karte eine der Stufenzahlen des Binärsystems steht: 1, 2, 4, 8, 16 oder 32 steht. 43=1x32+0x16+1x8+0x4+1x2+1x1=1010112. Damit ist der erste Schritt zum Verständnis des Tricks getan.

Auf der Karte mit der Zahl 32 oben links sind alle Zahlen enthalten, die in der Binärschreibweise 1x32 enthalten, z.B. nicht nur 43, sondern auch 44 (=1x32+1x8+1x4) usw. Die 44 steht aber auch auf der Karte mit der 8 oben links und auf der Karte mit der 4 oben links. Da diese Karte aber nicht ausgewählt wurde, kann 44 nicht die ausgedachte Zahl sein.
Alle Zahlen bis einschließlich 63 können im Binärsystem mit fünf Nullen oder Einsern geschrieben werden, z.B. 7=0001112, 44=1011002, 60=1111002 und 5=0001012. Auf der Karte mit der 32 oben sind alle Zahlen aufgelistet die an der ersten Position 1 haben (1xxxx), auf der mit 16 oben sind es alle Zahlen mit einer 1 an der zweiten Position (x1xxx), auf der mit 8 oben alle mit 1 an der dritten Position (xx1xx) usw., wobei x für 0 oder 1 steht.
Der Trick ist nur durch das Vermischen zweier verschiedener Stellenwertsysteme nicht sofort durchschaubar.

Das ist schon ein etwas seltsames und mystisches Muster, das die 16 von null bis fünfzehn nummerierten 4×4-Quadrate da bilden. Man sieht da auch ein Kreuz, zwei Hände, die es halten, oder handelt es sich um eine Art Kreuzworträtsel?
Natürlich nichts von alledem. Das erste Quadrat mit der 0 oben links enthält kein blaues Teilquadrat, das nächste Teilquadrat mit der 1 enthält ein blaues, noch logisch. Aber das Teilquadrat mit der 2 oben enthält auch nur ein blaues, zwei kleine blaue Quadrate enthält das Teilquadrat mit der 3 oben.
Zwei Farben, naturbelassen und blau, das könnt mit 0 und 1 zusammenhängen – also etwas mit dem Binärsystem zu tun haben. Versuch: blau = 1 und natur = 0. Nach einigen Versuchen kann man darauf kommen: Die binäre Schreibweise erfolgt hier nicht linear hintereinander, sondern im Uhrzeigersinn auf den vier kleinen Quadraten der Teilquadrate: Man beginnt mit dem rechts unten. Ist dieses Quadrat blau bedeutet das 1x1, ist es natur 0x1. Ist das linke untere Quadrat blau, heißt das 1x2, ist es natur dann 0x2. Sind also die beiden unteren Quadrate blau heißt das 1x1+1x2=3. Nun geht es im linken oberen Quadrat weiter mit 1x4 oder 0x4, je nach Farbe. Im oberen Quadrat rechts geht es dann mit 8 zu Ende.
Mit einer Binäruhr – das kann ich aus eigener Erfahrung bestätigen – kann man recht gut bei seinen Mitmenschen Aufmerksamkeit erregen. Aber auch feststellen, dass es 102 Gruppen gibt, nämlich die, die das Binärsystem kennen, und die, die es nicht kennen. In der Mathothek gibt es zahlreiche Uhren, darunter sind auch zwei ihr geschenkte Binäruhren.

Die erste ist eine Taschenuhr oder man kann sie auch an einer Kette um den Hals tragen, dazu gibt es eine passende Binärkette. Die roten Perlen trennen die Binärzahlen voneinander, die weißen Perlen bedeuten 1 und die schwarzen 0. So zeigt die Kette die Zahlen von 0 bis 15 in binärer Darstellung.

In der oberen Reihe der Taschenuhr werden durch Lichtpunkte angezeigt:
AM PM 8 4 2 1 H
32 16 8 4 2 1 M
In diesem Fall ist das Ablesen der Uhr ziemlich einfach, weil man die leuchtenden Stufenzahlen des Binärsystems nur addieren muss. Meistens erscheinen auf Binäruhren nur leuchtende oder nicht leuchtende Punkte, die Zweierpotenzen muss man sich dann selber dazu denken. Wichtig ist es dabei, dass man die Position der Einer erkennt (z.B. oben oder unten).
Auf dem Foto:
AM PM 8 4 2 1 H
32 16 8 4 2 1 M
Es war im Augenblick des Fotografierens 2:11 Uhr nachmittags.
Die andere Binäruhr ist etwas größer, aber vielleicht auch ein wenig komplizierter. Ihre Leuchtanzeige benutzt sowohl das Zehner- als auch das Zweiersystem. Auf dem nächsten Bild ist die Anzeigeseite dieser Uhr zu sehen, allerdings sind die zusätzlichen Angaben auf der Uhr (schwarze Beschriftungen) selbst nicht zu finden und dienen hier nur zur besseren Erklärung.

Die beiden hinteren Spalten zeigen die Sekunden, die mittleren zwei Spalten die Minuten und links die beiden Spalten geben die Stunden an. Bei den beiden Spalten stehen rechts die Einer und links die Zehner, so wie wir das gewöhnt sind. Die Angabe der Einer bzw. der Zehner erfolgt dann jeweils als Binärzahl. In der untersten Reihe zeigen die Leuchtpunkte die Einer an, darüber werden die Zweier angezeigt und danach – wenn es notwendig ist – die Vierer und die Achter. Im Augenblick des Fotografierens waren es 3 (=2×1+1×1) Stunden, 2(=2×1) Minuten und 41(=4×10+1×1) Sekunden.
Hier gelten weiterhin die Erläuterungen von oben. Die Uhr zeigt 3h, 3min und 2s oder 03:03:02 Uhr.

Nehmen wir einmal an, es wäre 11:35:27 Uhr, dann sähe das Bild so aus:
Bei den Stunden:
0 0 → 12
0 0 0 0 → 12
Bei den Minuten:
0 0 0 → 112
0 0 0 0 → 1012
Bei den Sekunden:
0 0 → 102
0 0 0 0 → 1112
Natürlich ist das Ganze um 90° gegen den Uhrzeigersinn zu drehen , sodass der erste Leuchtpunkt die Einer darstellt.
Diese Notation ist im Grund genommen uralt. Stammt doch unsere Zeiteinteilung aus Mesopotamien und dem dort entwickelten Sexagesimalsystem, einer Zahlschreibweise mit einem Stellenwertsystem, das nicht auf der Zehn und auch nicht auf der Zwei aufbaute, sondern auf der 60. In der Keilschrift gab es zum Schreiben von Zahlen einen schmalen senkrechten Nagel oder Keil für die Zahlen 1 bis 9 und einen breiteren waagrechten Keil für die Zehn. Ohne diese Mischung hätte man 59 schmale Nägel in die Tontafel drücken müssen, wenn man 59 Einer oder 59 Sechziger usw. hätte schreiben wollen. Dagegen genügten mit dieser gemischten Schreibweise fünf waagrechte Keile und neun senkrechte Nägel.


Gibt es die abgebildeten Uhren irgendwo käuflich zu erwerben?
LG Knut Leiß