Wie können wir helfen?
Wenn jüngere Besucher in der Mathothek das folgende Exponat entdecken, dann folgt erst einmal ein fettes Grinsen.

Dann bei dem Hinweis, dass man auf diese Weise mit den Fingern einer Hand die Zahlen von null bis 31 und mit zwei Händen sogar bis 63 zeigen kann, wird aus der leicht peinlichen Reaktion ein fragendes Staunen. Obwohl der Computer natürlich keine Finger besitzt, arbeitet er genau mit diesem Zahlensystem. Es funktioniert mit genau zwei Zeichen oder Ziffern: Finger gestreckt oder nicht, 1 oder 0. Deswegen nennt man dieses Zahlsystem Binär-, Dual- oder Zweiersystem. Für unser in Fleisch und Blut übergegangenes Dezimal- oder Zehnersystem benötigen wir bekanntlich 10 Ziffern oder Symbole und wahrscheinlich ist es auch aus den zehn Fingern unserer Hand entstanden. Falls Dir keinen Spaß macht, selbst herauszufinden, wie die Zahlendarstellung mithilfe der Finger und dem Binärsystem funktioniert, so kannst Du die Plastikkärtchen umdrehen und Dir so helfen lassen.
Hier liegt der Schlüssel zum Verständnis des Binärsystems. Das Binärsystem ist wie unser Dezimalsystem ein Positionssystem. Zum Beispiel bedeutet 3056 die Zahl, die aus drei Tausendern plus 0 Hundertern plus fünf Zehnern und sechs Einer besteht. Während beim Dezimalsystem die Zehnerpotenzen die Stufenzahlen sind, sind das beim Binärsystem die Potenzen der Zwei, also 20=1, 21=2, 22=4, 23=8, 24=16 usw. Schauen wir uns die Zahlen 5, 7 und 24 einmal im Binärsystem an:
5=1x4+0x2+1x1
7=1x4+1x2+1x1
24=1x16+1x8+0x4+0x2+0x1

Wenn ich also 5, 7, 24 im obigen dualen Fingersystem darstellen will, muss ich für die Fünf den Daumen (ein Einer), nicht den Zeigefinger (kein Zweier) und noch den Mittelfinger (ein Vierer) zeigen, für die Sieben braucht man den Daumen (Einer), den Zeigefinger (Zweier) und den Mittelfinger (Vierer). Für die 24 streckt man nur den Ringfinger und den kleinen Finger (Einer), d.h. 24 setzt sich aus einmal 16, einmal 8, nullmal 4, nullmal 2 und nullmal 1 zusammen.

Da man ja nicht vor jedem “Zahlen Zeigen” sicherheitshalber sich noch schnell die Hände waschen kann, gibt es seit langer Zeit eine einfache binäre Schreibweise. So schreibt man die Fünf im Binärsystem 1012, die Sieben 1112 und die 24 als 110002. Somit kann man jede Zahl im Binärsystem mit nur den Ziffern 0 und 1 schreiben. Die Einfachheit dieses binären Zahlensystems wird mit der sehr schnell wachsenden Länge der Ziffernfolgen bezahlt. Was aber den Computer nicht zu stören scheint.

In Schwarz-Weiß-Land gibt es einen Juwelier der Gold- und Silberketten aus vorgefertigten Teilen zu einem Spottpreis anbietet. Das Angebot gilt nur, wenn die Kundin eine Kette möchte, die der Goldschmied aus den fertigen Teilen zusammensetzen kann, ohne das ein Teilstück zweimal vorkommen darf, und er keine Gliederfolge öffnen muss.
Hier ist eine Übersicht der fest zusammengefügten Teilstücke:

Das längste Teilstück besteht aus 32 Gliedern. Es folgen Teilstücke mit 16, 8, 4, 2 und 1 Gliedern. Die nächste Kundin möchte eine Kette mit insgesamt 23 Gliedern. Der Verkäufer legt ihr die folgenden Teilstücke vor:

Da unsere Kundin mathematisch gebildet ist, überprüft sie kurz, dass 23 im Dualsystem 101112 ist und stimmt zu.

Wie viele Glieder hat die längste Kette, die der Juwelier zu seinen Bedingungen herstellt? In Binärschreibweise ist die Antwort 1111112 Glieder.
Schreibe Deine Kettenwünsche im Binärsystem auf.

Dieses rot-blaue Exponat dient dem Messen im Dualsystem. Das kleinste Stück ist 1 cm lang. Jedes weitere Stück links daneben ist doppelt so lang wie sein rechter Nachbar, d.h. die anderen Holzsäulen haben die Längen 2 cm, 4 cm, 8 cm, 16 cm, 32 cm, 64 cm und 128 cm.

Als Beispiel wurde hier eine gerollte Karte in ihrer Verpackung genommen. Für die Röhre benötigte man ein 64er, ein 32er, ein 4er und ein 1er Stück. Damit ist die Röhre 1100101 cm lang, allerdings in binärer Schreibweise. Im vertrauten Dezimalsystem sind das 101 cm. Es gibt noch ein paralleles Objekt, das weniger gefährlich ist, weil die Stäbe nicht aus hartem Holz, sondern aus Stücken von Schwimmnudeln bestehen:

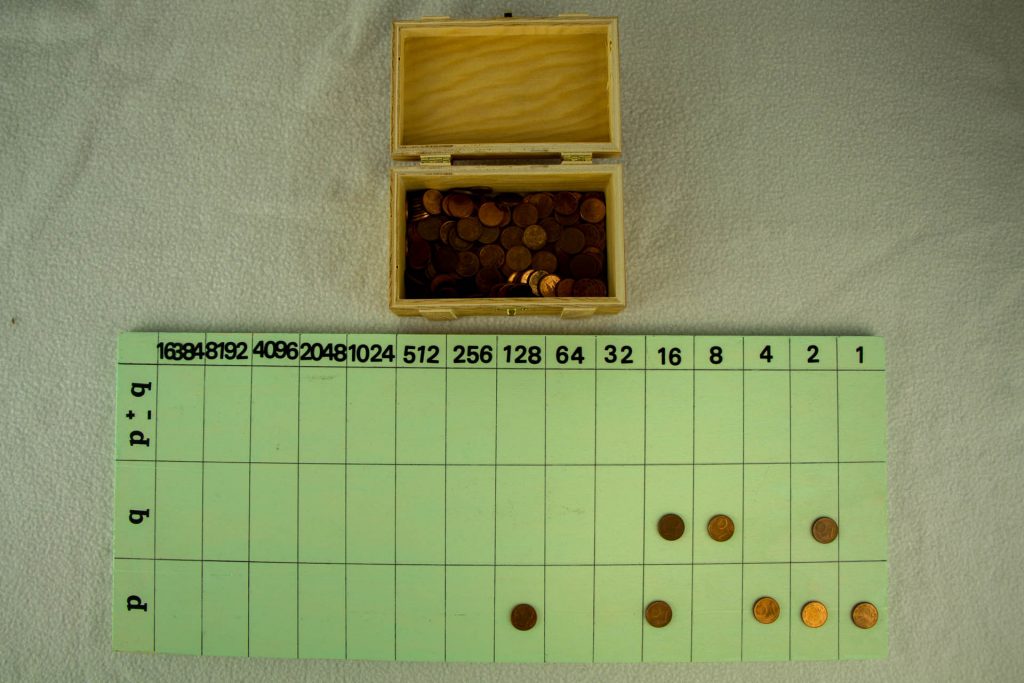
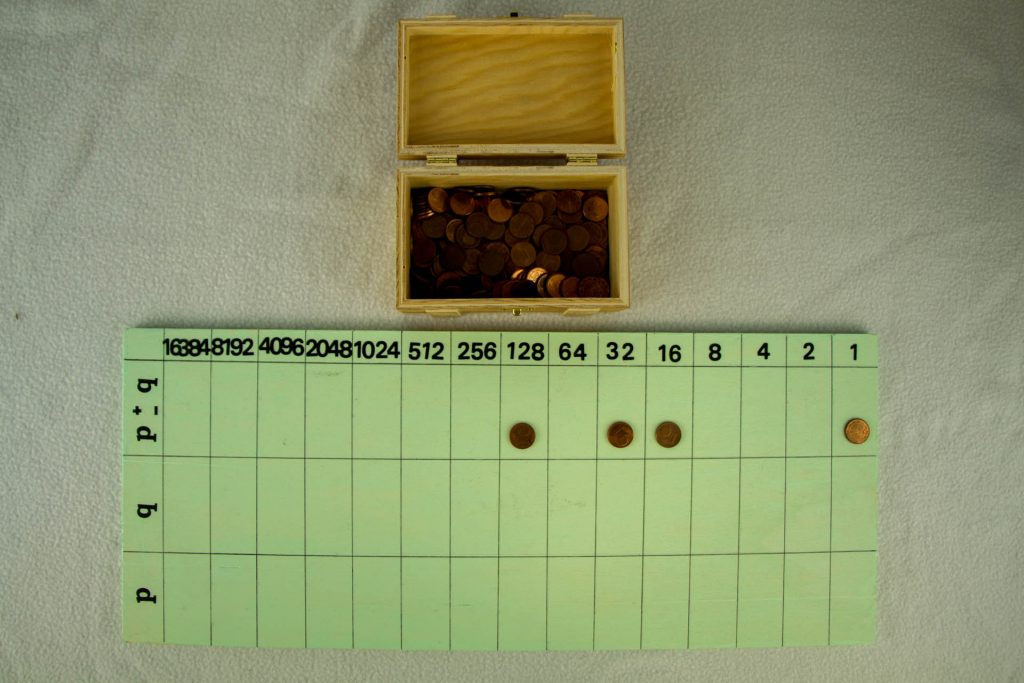
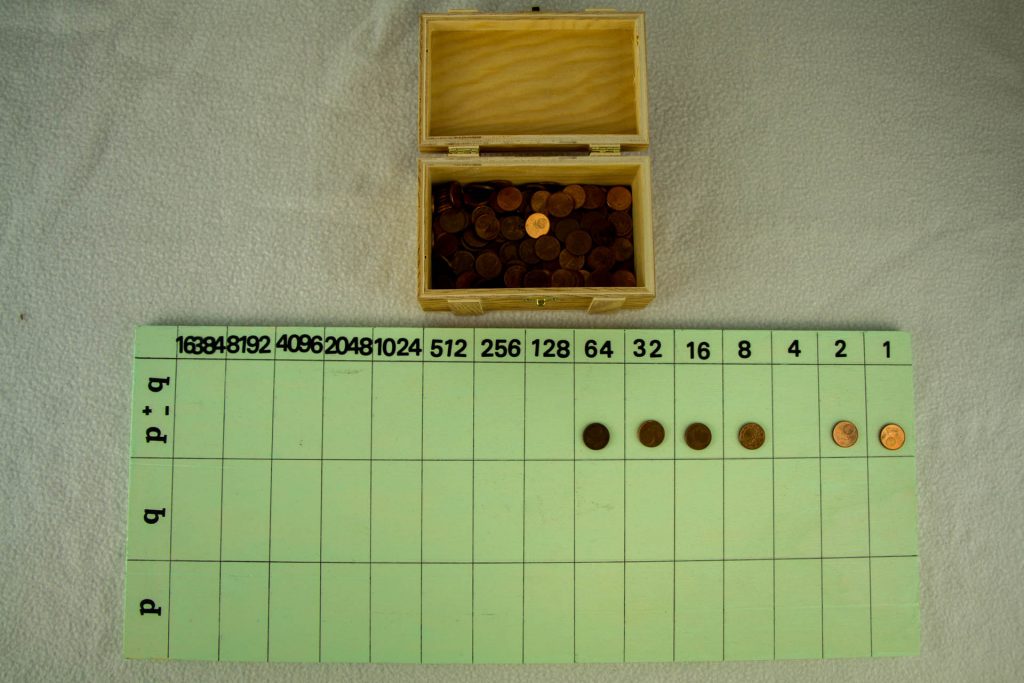
Um im Binärsystem zu rechnen, d.h. im Wesentlichen zu addieren und subtrahieren, gibt es in der Mathothek ein Rechenbrett und Rechenpfennige. Wie es dann zum Addieren benutzt werden kann, zeigt das Beispiel 151+26=100101112+110102.
Zuerst legt man die Rechenpfennige der beiden Zahlen in die Zeilen für die Summanden p und q, schiebt dann die Pfennige spaltenweise in die Summenzeile (oben) und korrigiert die Überträge.
Wir erhalten dann 101100012=17710.
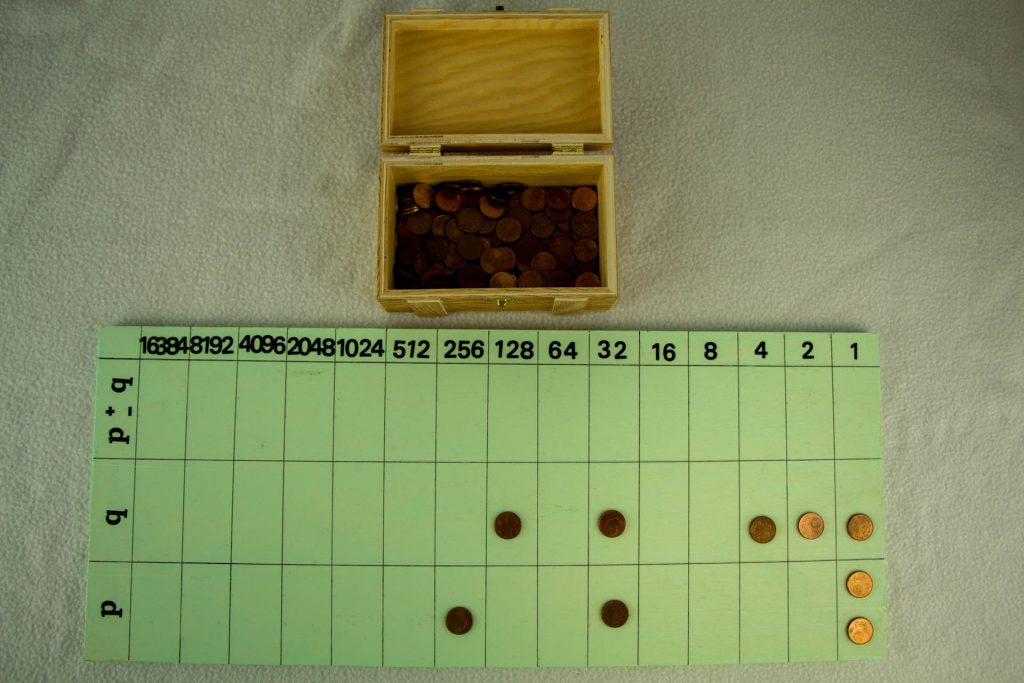
Im folgenden Beispiel geht es um die Subtraktionsaufgabe 290-167, p=29010=1001000102 und q=16710=101001112
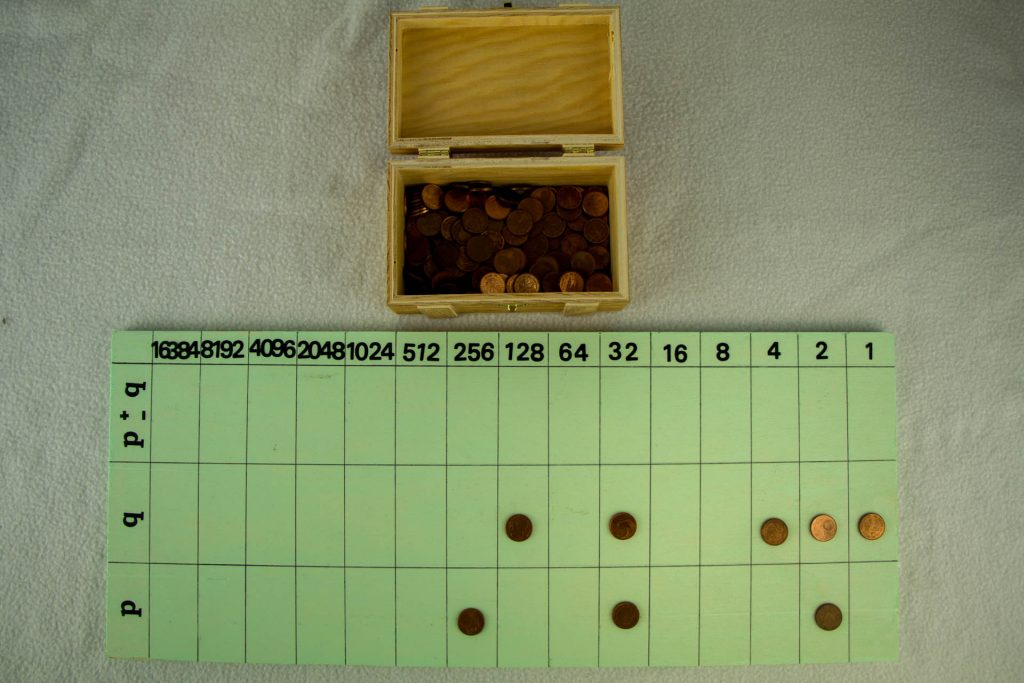
Schon beim ersten Schritt gibt es ein Problem. In der Einer-Spalte soll von keinem Einer einer weggenommen werden, was aber nur möglich wird, wenn man den Zweier von p in zwei Einer umwandelt. Dann wandert ein Einer in die Ergebnis-Spalte.
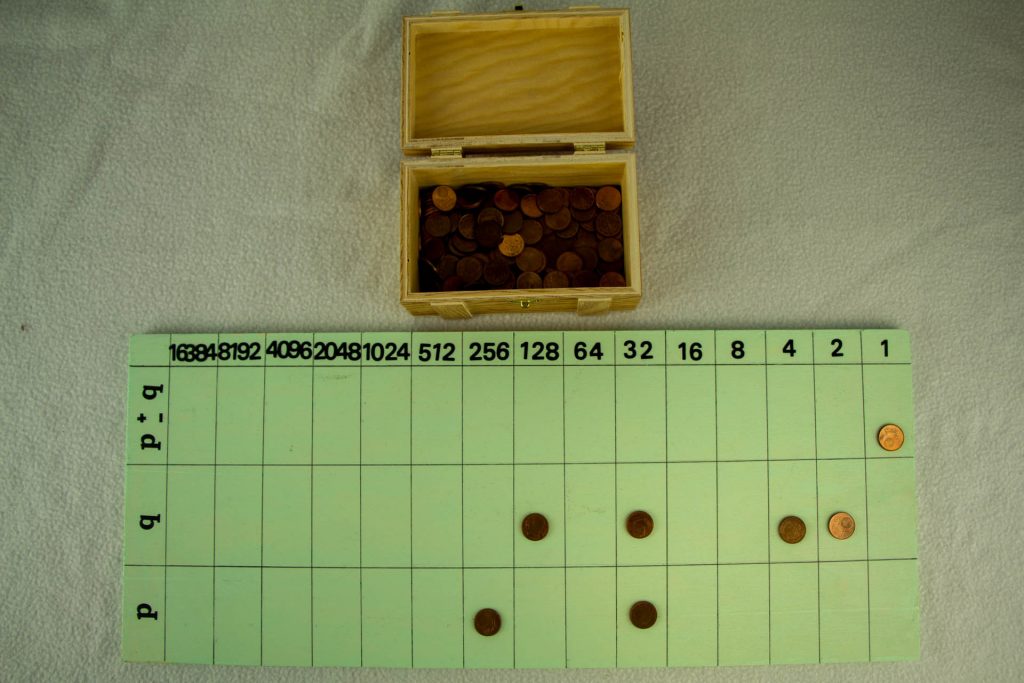
In der Zweier-Spalte taucht dasselbe Problem auf: Von keinem 2-er soll einer weggenommen werden. Also heißt es umtauschen, und zwar ein 32-er in zwei 16-er, ein 16-er in zwei 8-er, ein 8-er in zwei 4-er und zum Schluss noch ein 4-er in zwei 2-er. Dann sieht das Zwischenergebnis so aus:
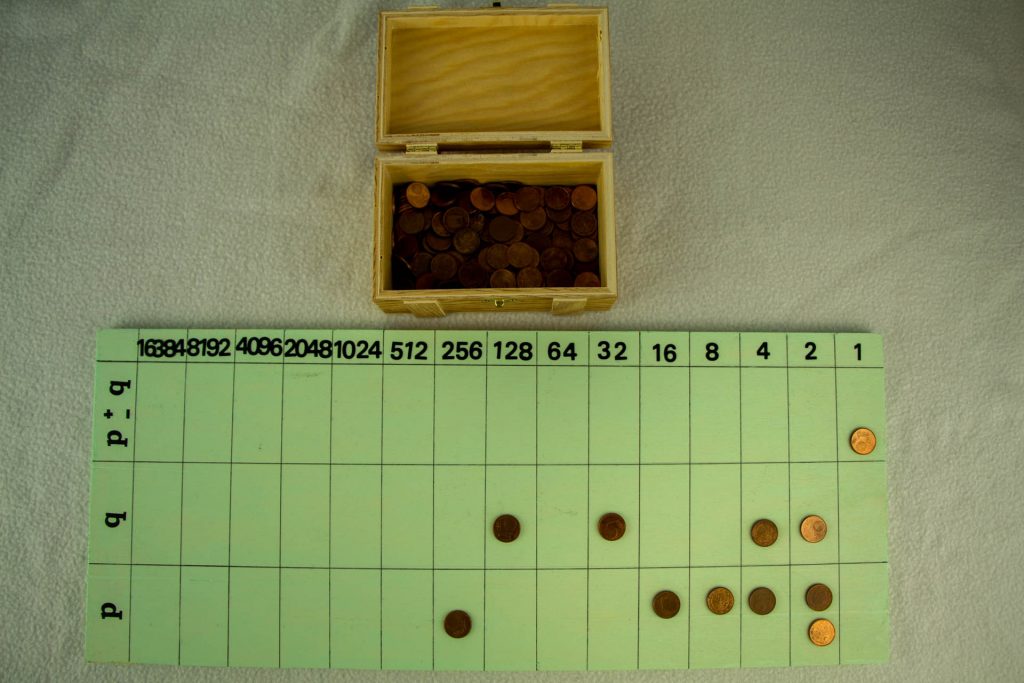
Jetzt kann subtrahiert werden und man erhält Folgendes:
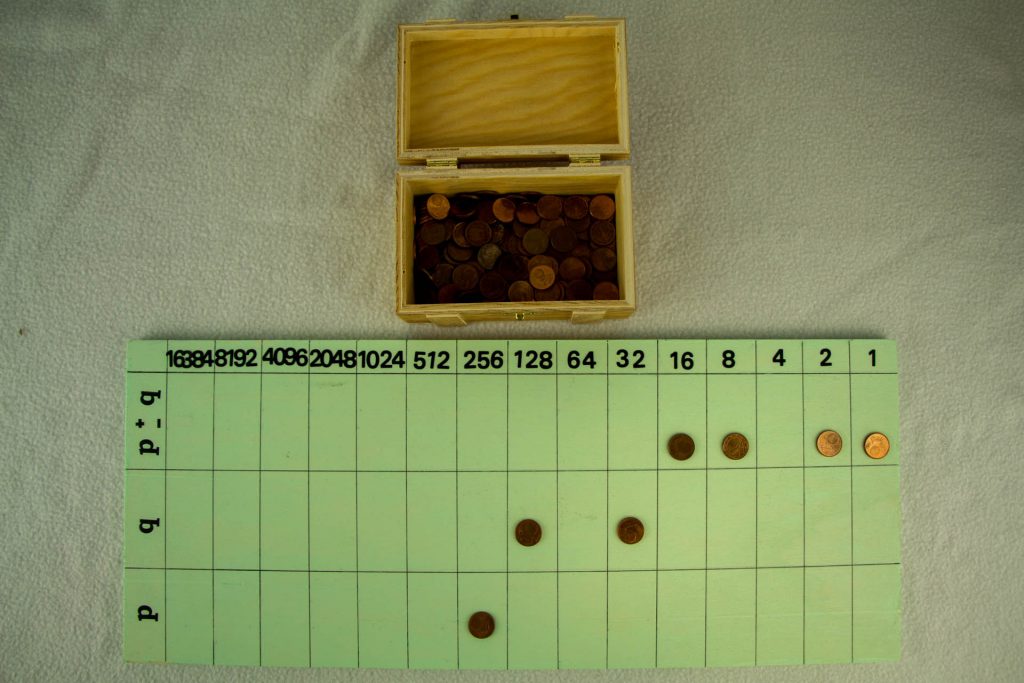
Schon wieder tritt das inzwischen bekannte Problem auf und wird durch den Umtausch des 256-er gelöst:
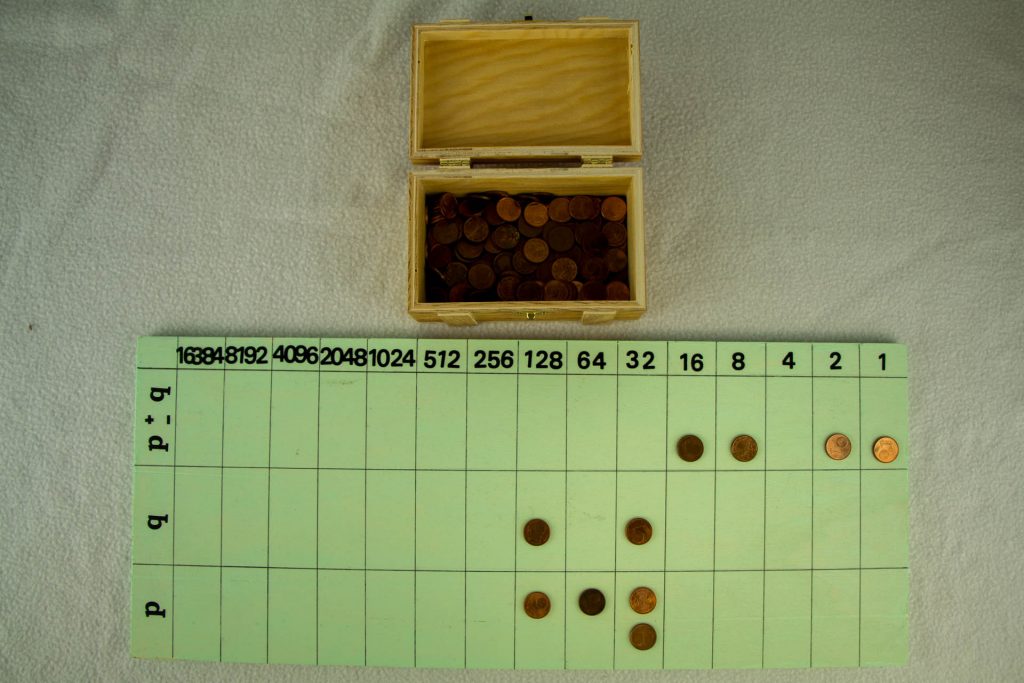
Endergebnis beträgt 11110112 oder im Dezimalsystem 123.
Dieses Beispiel soll nicht abschrecken, sondern das Umwandeln wirklich gründlich vorführen.
Die Nutzung der drei Zeilen des Rechenbretts ist auch anders möglich, z.B. Minuend in die oberste Zeile, Subtrahend in die zweite Zeile und das Ergebnis (=Differenz) in die dritte Zeile eintragen. Das hat den Vorteil, dass man gut die Probe machen kann.