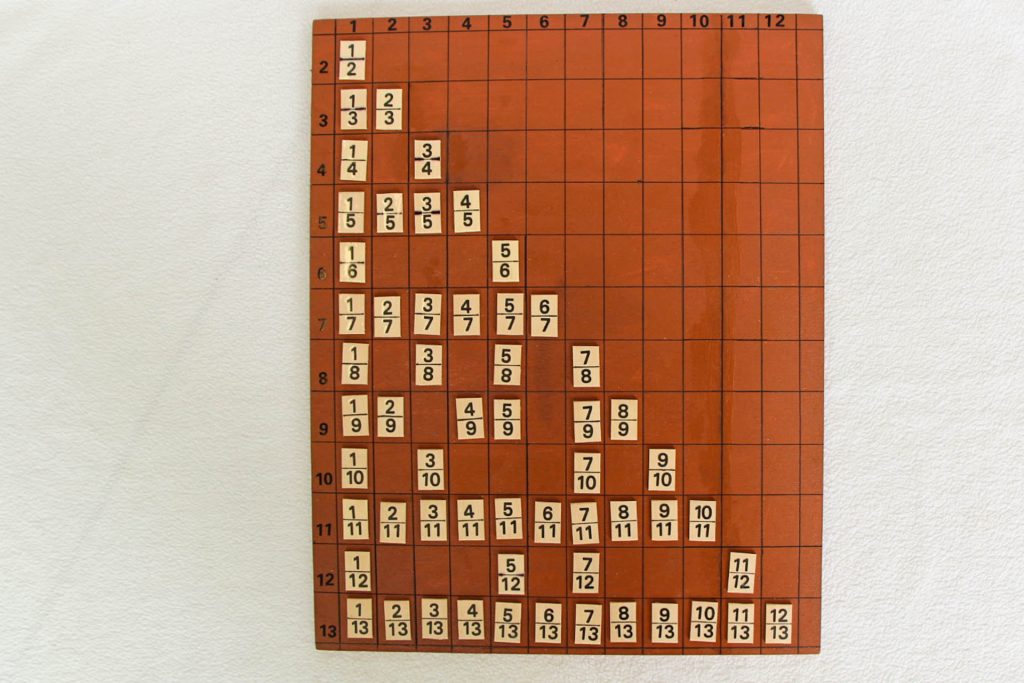Am Samstag, dem 1. Oktober 2022, wird die Mathothek wieder von 11:00 bis 17:00 Uhr für alle Interessierten geöffnet sein.
Eintritt: nur ein wenig Neugierde, Aufgeschlossenheit und Experimentierfreude.
Diese Fotos von drei Objekten der Mathothek werden bei den meisten Betrachtern wohl sehr bald Assoziationen zum “Unendlichen” auslösen:
Mit zahlreichen Exponaten der Mathothek lässt sich ein anschaulicher Weg zur Faszination des “Unendlichen” gehen. Deswegen gibt es für diesen Samstag als besonderes Angebot, sich mithilfe einiger Exponate der Mathothek dem “Unendlichen” zu nähern.
So zeigen z.B. die obigen Beispiele, dass wir im Alltag das Wort “unendlich” oft nur dazu benutzen, um zu sagen, dass eine bestimmte Menge sehr viele Elemente besitzt, die wir zwar prinzipiell zählen könnten, aber die große Mühe für diesen Aufwand nicht aufbringen wollen. Oder in uns weckt das Erkennen eines Prinzips das Gefühl, dass wir etwas “unendlich” fortsetzen könnten.
Auch bei den Bildern, die auf den Fotos unten zu sehen sind, treten nicht wirklich unendlich viele Elemente auf. Aber aus der Entdeckung einer dahinterstehenden Idee, eines Musters, einer Folge setzen wir mental das Bild unendlich fort.
Ein Beispiel: Nach kurzem Betrachten des unteren Bildes erkennt man die Idee, die dahintersteckt:
Schrittweise wird einerseits die Anzahl der Kreise einer Reihe (Farbe) verdoppelt und werden andererseits die Durchmesser halbiert. Gedanklich lässt sich diese Erkenntnis dann gedanklich unendlich fortsetzen. Was ist aber, wenn wir uns einerseits die Längen aller Umfänge der Kreise der einzelnen Reihen überlegen und andererseits die Summen der Flächeninhalte aller Kreise einer Reihe betrachten?
Das folgende Bild zeigt uns anschaulich, dass die Summe 1/4+/16+1/64+… aus unendlich vielen Summanden den Wert 1/3 besitzt:
Selbstverständlich gibt es “unendlich” viele natürliche Zahlen, und zwar in dem Sinne, dass es keine größte geben kann. Aber es gibt auch genauso viele rationale Zahlen, wie ein Exponat der Mathothek zu erkennen hilft:
Nun könnte man denken, dass dieses “Unendlich” das Ende der Fahnenstange sei. Aber das ist nicht der Fall, wie uns die Menge aller reellen Zahlen zeigt. Diese Zahlenmenge ist natürlich unendlich, aber doch wesentlich größer als die Menge der rationalen Zahlen. Sie lässt sich beweisbar prinzipiell auch in keiner unendlichen Liste auflisten.
Bei Interesse bieten die Experimente der Mathothek eine sehr breite und reiche Palette an Zugängen zum Thema “unendlich”.
Aber natürlich kann jeder Besucher der Mathothek nicht nur mit diesen Bausteinen experimentieren, sondern auch mit allen anderen der über 1000 Exponate der Mathothek. Einen sehr großen Teil dieser Objekte könnt Ihr schon im Vorfeld virtuell kennenlernen, indem Ihr unseren Katalog auf der Website der Mathothek besucht: mathothek.de.
Mathothek – der sinnliche Zugang zur Mathematik!