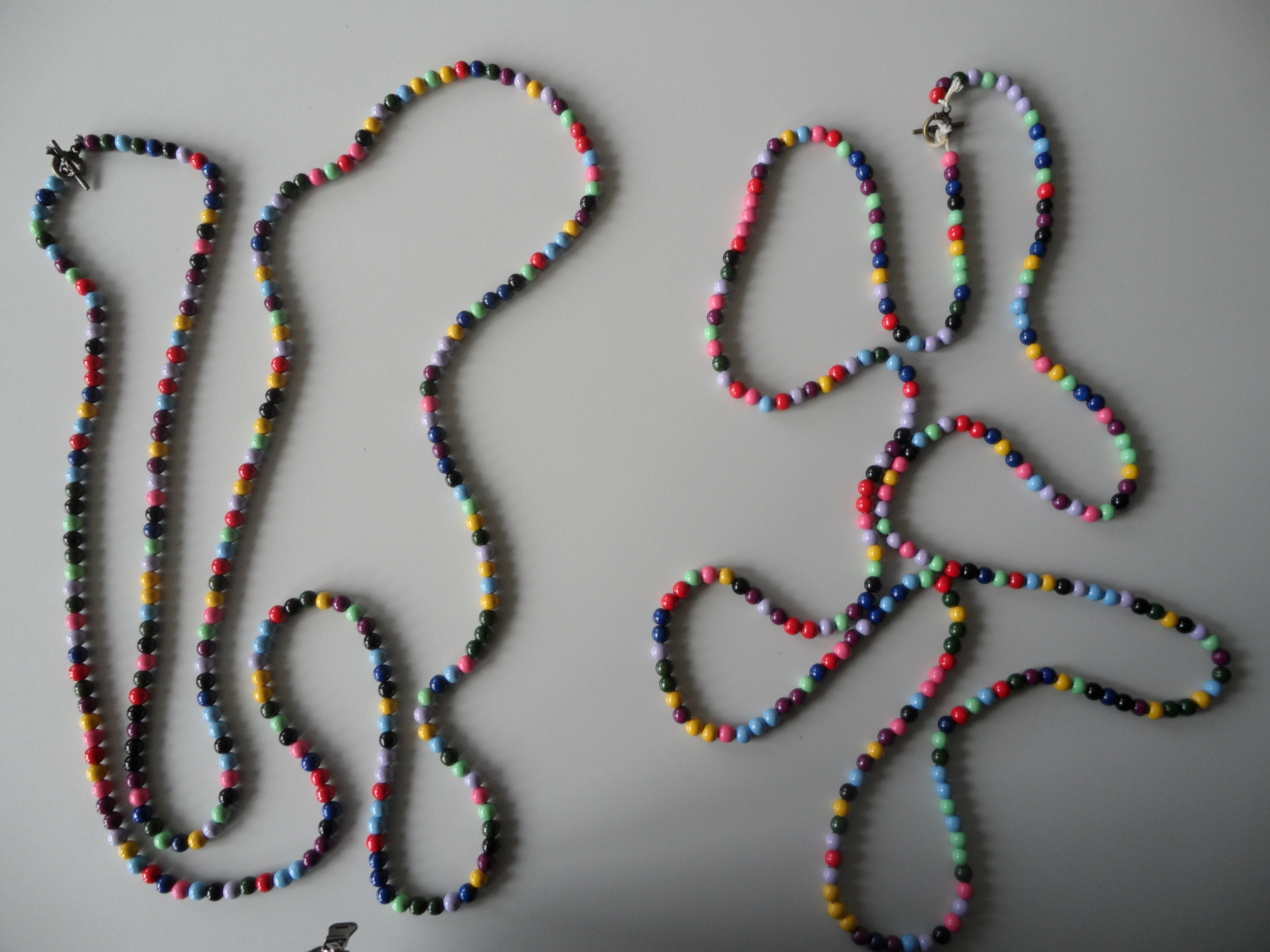Besuch aus Bitche
Während des jüngsten Besuchs unserer Austauschschülerinnen und -schüler aus Bitche (Frankreich) in der Mathothek – ein fester Baustein in dem Besuchsprogramm seit langem – ergab sich die Gelegenheit zu einer “kleinen Führung” für Frau Heilhecker, Begleiterin für die französische Gruppe und Deutsch- und Französischlehrerin unserer Schule. Die begeisterten und intensiv beschäftigten Franzosen machten diese kleine “Sonderführung” möglich. Die ausgewählten Exponate mit den entsprechenden Hinweisen und Erklärungen sollen hier allen Interessierten vorgestellt werden, aber auch das großartige Dankeschön der Besucherin – das Gedicht Unendlichkeiten – diesen Beitrag krönend beenden. Dieser Beitrag soll die Breite und Tiefe, geistige Offenheit und inspirierende Kraft der Mathothek zeigen.
Bleibt nur noch anzumerken, dass es zu jeder der vier Stationen noch reichlich weitere, hier nicht gezeigte interaktive und Anschauungsobjekte in der Mathothek gibt.
Erste Station: Magie der Sieben
Die Zahl sieben spielt seit ewigen Zeiten eine besondere Rolle in den Mythen, Religionen und Sagen der Menschen. So werden auf der Himmelsscheibe von Nebra, der bisher ältesten Himmelsdarstellung, die Plejaden mit sieben Sternen dargestellt (Siebengestirn), obwohl man mit besseren Augen auch acht oder mehr bzw. mit schwächeren auch weniger Sterne erkennen kann. Die fünf Planeten (Merkur, Venus, Mars, Jupiter und Saturn), die man mit bloßem Auge sehen und beobachten kann, und die beiden größten Himmelskörper Sonne und Mond ergaben für die Menschen in der Frühzeit sieben besondere Erscheinungen am Himmelszelt. Im Gegensatz zu der riesigen Zahl der Fixsterne, die sich zu festen Sternbildern ordnen ließen, vollführten die beweglichen Sterne ganz besondere Bewegungsabläufe, aus denen man den Willen der Götter zu erkennen glaubte oder die Planeten selbst mit Göttern gleichsetzte. Noch heute erinnern die Namen der Wochentage daran.
In allen großen Religionen der Welt spielt die Sieben eine besondere Rolle. So enthält das “Gebet des Herrn”, das Vaterunser, sieben Bitten, gibt es bei den Katholiken die sieben Sakramente, die sieben Todsünden, die sieben Kardinaltugenden usw. Im Neuen Testament, und zwar in der Offenbarung des Johannes, gibt es eine Fülle der Verwendungen der Sieben. Ein interessanter mathematischer Zusammenhang der Sieben mit der Zahl des Tieres 666:
22+32+52+72+112+132+172=666 (Quadrate der ersten sieben Primzahlen) !!!
Im Mithraskult gab es sieben Weihegrade, im Islam muss der Pilger in Mekka die Kaaba siebenmal umrunden und im Buddhismus stellt Buddha eine siebenstufige Skala des Kleinerwerdens auf.
Im Judentum spielt die Sieben nicht nur bei der Erschaffung der Welt eine Rolle, bei Sabat- und Erlassjahr, sondern auch in vielen weiteren Zusammenhängen. Vermutlich hat hier der starke Einfluss der sehr alten Kultur des Zweistromlandes (Mesopotamien) gewirkt, in der die Magie der Zahl sieben eine große Verbreitung hatte. Natürlich hat das aus dem Judentum hervorgegangene Christentum entsprechend die magische Wirkung der Sieben weiter verwendet.
Aus den Mythen und Religionen fand die Sieben ihren Weg in die Sagen, Märchen und Erzählungen der Völker. So z.B. im alten Griechenland und Rom. In den folgenden Bildern finden sich Anspielungen auf Märchen der Brüder Grimm: Der Wolf und die sieben Geislein, Schneewittchen und die sieben Zwerge, Hans im Glück und Der Bärenhäuter.
Das sind nur einzelne Beispiele für eine riesige Fülle von möglichen.
Zweite Station: Fibonacci-Zahlen
Eine fast magische Zahlenfolge bilden die Fibonacci-Zahlen: 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, … . Ihr Baugesetz ist leicht zu durchschauen: Die Summe zweier aufeinander folgender Zahlen ergibt die nächste Zahl in der Folge: 1+1=2, 1+2=3, 2+3=5 u.s.w. Diese berühmte Zahlenfolge wurde nach dem italienischen Kaufmann und Mathematiker Fibonacci benannt und spielt in der Mathematik, in der Natur und in der Kunst eine wichtige Rolle.
Ein überzeugendes Beispiel aus der Natur sind die Anzahlen der parallelen Spiralen bei den Zapfen von Nadelbäumen: Auf den Fotos sind es bei dem Pinienzapfen die Zahlen 5 und 8, bei dem Fichtenzapfen 5, 8 und 13. Es gibt noch eine Menge solcher Beziehungen, z.B. bei der Ananas und der DNA des Menschen. Hier beträgt der Abstand der kleinen Furche 13 Å und der großen Furche 21 Å, ebenfalls zwei Fibonacci-Zahlen.
Im Wiesbadener Museum gibt es einen Raum, der zwei Werken des Künstlers Mario Merz gewidmet ist: “Spiraltisch mit Iglu” und “Gambe che corrono” (Fotos in der Mathothek). Beide Werke enthalten Neonzahlen, und zwar beide Male Anfangszahlen der Fibonacci-Folge. Sie symbolisieren hier den Wachstumsprozess von Natur und Kultur, betonen das Aufbauende in diesem Fortschreiten.
Bei den beiden Ketten mit Holzperlen geht es um zwei Darstellungen der ersten Fibonacci-Zahlen
Dritte Station: Unendlichkeit
Schon bei der Fibonacci-Folge stößt man auf die Unendlichkeit: Jeder erkennt sofort, dass es keine größte solche Zahl geben kann, dass es daher unendlich viele Fibonacci-Zahlen geben muss. Das Prinzip des schrittweisen Aufbaus dieser Zahlen, lässt die Folge für uns “wie fertig” als Zahlenmenge erscheinen. Die Beschäftigung mit dem Unendlichen ist so recht schon immer ein Motor der Mathematik gewesen.
Beim ersten Bild geht es um eine Folge von größer werdenden Quadraten, die einerseits mit dem Satz von Pythagoras zusammenhängen, und zwar so, dass ihre Flächeninhalte andererseits den oben beschriebenen Fibonacci-Zahlen entsprechen. Bemerkung einer jüngeren Schülerin: “Ich finde es so toll, wie aus lauter eckigen Quadraten und rechten Winkeln so etwas Pflanzilches entsteht”.
Auch bei der Koch’schen Schneeflockenkurve lässt das Bild die Konstruktionsschritte gut erkennen. Sie ist ein besonders interessantes Tier aus dem Funktionenzoo der Mathematik.
Bei Bild drei kann man – ohne groß zu rechnen – herausfinden, dass die Summe der Flächeninhalte aller unendlich vielen gelben Dreiecke gerade Mal ein Drittel des gesamten Dreiecks und damit die unendliche Summe 1/4+1/16+1/64+1/256+…=1/3 beträgt.
Beim fünften Bild lässt sich leicht einsehen, dass in jeder neuen Folge von Kreisen ihre Anzahl sich verdoppelt, ihr Durchmesser sich aber halbiert, und damit die Summe der Umfänge aller Kreise auf jeder Stufe gleich dem Umfang des größten Kreises am Anfang ist. Andererseits ist aber leicht einsehbar, dass die Summe aller Kreisfächeninhalte zu jeder nächsten Stufe kleiner und kleiner wird, sie sich immer mehr dem Wert null nähern. Für unsere Alltagserfahrung ein Paradoxon.
Die beiden Ketten auf Bild sechs enthalten Perlen mit zehn verschiedenen Farben. Auch nach längerem Suchen lässt sich kein Prinzip in ihren Anordnungen finden. Die beiden Muster scheinen sich sehr ähnlich zu sein. Dennoch bringt die Erläuterung ihrer Entstehung großes Erstaunen mit sich: Jede Perlenfarbe entspricht bei beiden Ketten einer der Ziffern 0 bis 9. Bei einer der Ketten wurde die Reihenfolge aber zufällig mit einem “Zehnerwürfel” festgelegt, bei der anderen wurden für die Reihenfolge der Farben dagegen die Nachkommastellen der Zahl π genommen.
Die letzte Kette besteht aus ca. 70 Holzperlen, die alle verschieden sind, keine zwei Perlen sind gleich. Das ist noch nichts Besonderes. Zwei Ketten, die dieselben Perlen umfassen, aber sich in der Anordnung dieser Perlen unterscheiden, stellen zwei verschiedene Permutationen dar. Und jetzt: Fragt man sich nun nach der Anzahl aller möglichen Permutationen, so lautet die Antwort, es sind über 10100 – eine Zahl mit einer Eins und danach 100 Nullen. Im Alltag würden wir hier selbstverständlich von einer unendlich großen Zahl sprechen. Mathematisch handelt es sich hier aber um keine Erscheinung des Unendlichen.
Vierte Station: Der Goldene Schnitt
Dividiert man zwei aufeinander folgende Fibonacci-Zahlen, und zwar die kleinere durch die größere, so nähern sich die Ergebnisse immer mehr dem Wert des Goldenen Schnitts φ = 0,61803398874989… , eine irrationale Zahl mit unendlich vielen Kommastellen, ohne Periodizität, die sich nicht durch einen Bruch darstellen lässt.
Der goldene Schnitt ist ein besonderes Verhältnis zweier Strecken.
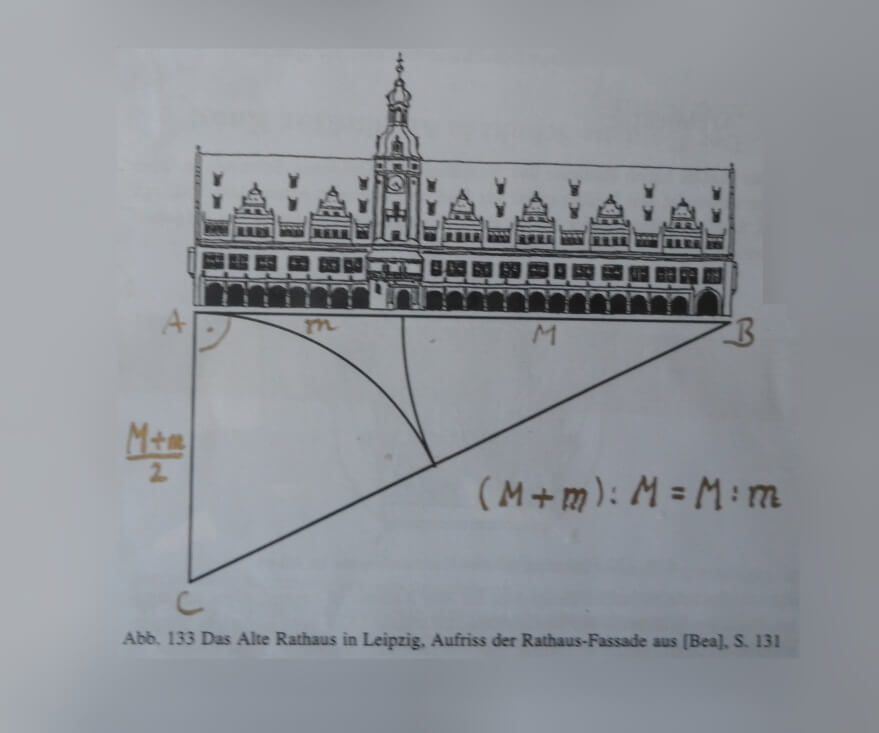
Goldener Schnitt: Ist eine Strecke so geteilt, dass die kürzere Teilstrecke sich zur längeren Teilstrecke so verhält, wie die längere Teilstrecke sich zur Gesamtstrecke verhält, dann ist die gegebene Strecke im Verhältnis des goldenen Schnitts geteilt worden, es stehen die beiden Teilstrecken im Verhältnis des goldenen Schnitts. Wenn mit m die kürzere Teilstrecke (Minor) und mit M die längere Teilstrecke (Major) bezeichnet wird, dann stehen m und M im Verhältnis des goldenen Schnitts genau dann, wenn m : M = M : (m + M) gilt. Im Zusammenhang mit der Fassade des Leipziger Rathauses lässt sich die übliche Konstruktion des goldenen Schnitts verfolgen.
Auf dem ersten Bild ist eine besondere Teilung im goldenen Schnitt nach dem Künstler Jo Niemeyer dargestellt.
Auf dem nächsten Bild kann man erkennen, wie man mit einem speziellen Zirkel leicht überprüfen kann, ob eine Teilung im goldenen Schnitt vorliegt. In dem Fall zeigt der Zirkel, dass bei der ” Geburt der Venus” von Botticelli, der Nabel der Göttin – wie es auch die Regel bei jedem Menschen der Fall ist – ihre Größe im goldenen Schnitt teilt.
Aber auch bei der EC-Karte oder fast allen Kundenkarten lässt sich leicht feststellen, dass Länge und Breite der Karten im Verhältnis des goldenen Schnitts stehen.
Die drei letzten Abbildungen zeigen sehr überzeugende Verwendungen des golden Schnitts berühmter Maler in drei bekannten Bildern. Zuerst “Mère et enfant” von Marc Chagall und das Mutter-und-Kind-Bild von Pablo Picasso: Teilt man die Höhe und Breite der Bildfläche im goldenen Schnitt, so spürt man die von allen Sinnen getragene Liebe und engste Beziehung zwischen der Mutter und ihrem Kind. Um Liebe, Zuneigung und Schutz geht es auch in Picassos Bild mit dem Kind und der Taube: Auch in diesem Bildaufbau geben die beiden Schnittlinien den Hinweis auf die zentrale Aussage des Bildes.
Bleibt zum Schluss noch das Bild “Kreidefelsen auf Rügen” von Caspar David Friedrich. Dieses Bild gehört sicher zu den bekanntesten Gemälden dieses berühmten Malers der Romantik. Ein Maler, der den goldenen Schnitt nicht nur kannte, sondern ihn auch in seinen Zeichnungen und Gemälden sehr oft verwandt hat. In diesem Bild ist der Durchblick auf das blaue Meer von den weißen Kreidefelsen in Form einer Parabel begrenzt, einer zum Himmel hin geöffneten Parabel. Die eingezeichnete schwarze Linie ist die zur Gleichung y = 1,6x2 gehörende Parabel. Sie passt besser als andere Parabeln zur Erfassung des Meeresausblicks. Da die Zahl des goldenen Schnitts Φ = 1.618033988… beträgt, lässt dies einen staunend und fragend zurück. Nicht erstaunlich ist dagegen, die Form des Fensters durch die Kreidefelsen: die Parabel selbst. Sie macht im Hinblick auf die Auffassungen der Romantiker Sinn. Die Maler der Romantik haben immer wieder Landschaften und Natur gezeichnet und gemalt. Aber nicht wie eine Fotokamera, sondern so verändert, dass das Gezeichnete oder Gemalte ein Aussage vermittelt. Dabei geht es um die grundsätzlichen Fragen des Menschen: Wo komme ich her? Wo gehe ich hin? Das Verlorensein oder auch Aufgehobensein des Menschen. Natürlich auch um Fragen nach Ewigkeit und Gott.
Eine Parabel ist ein Kegelschnitt, so wie es auch der Kreis, die Ellipse und die Hyperbel sind. Im Unterschied zur Ellipse, die zwei endliche Brennpunkte besitzt, hat die Parabel zwar auch zwei Brennpunkte, aber nur einen im Endlichen. Der zweite Brennpunkt der Parabel liegt im Unendlichen. Folglich ist die Parabel ausgezeichnet geeignet, die Transzendenz im Bild auszudrücken. Dazu kommt noch die Farbe blau. Blau ist die Farbe der Romantik (“Die blaue Blume”): Sie steht für Ferne, Sehnsucht, Freiheit und Unendlichkeit. Noch bei Marc Chagall steht diese Farbe für das Göttliche, zum Beispiel in den Chagallfenstern in St. Stephan in Mainz.
Mathematik und Lyrik sind beim breiten Publikum keine Quotenbringer, wie Sport und Ernährungsmoden beispielsweise. Der Mathematik traut man immerhin noch einen gewissen Nutzen zu: Man hat schon Mal gehört, dass in seinem Smartphone jede Menge Mathematik stecken soll.
Lyrik und Mathematik sind durch vieles verbunden, so durch die Vorliebe für Eleganz und Schönheit, aber noch mehr durch ihren Bezug zur Sprache. Durch die völlig andersartige Verwendung und Ausformung ihrer Sprachen sind sie aber auch wiederum extrem getrennt.
Hier eine versöhnliche Verbindung von beiden.
-
Unendlichkeiten
von Monika Heilhecker
-
Der Zahlen Mythen,
Unendlichkeiten,
Sternbilder – Märchen
durch der Götter Lenkung in Schattierungen.
Gleichnisvolle Bildreflexe im goldenen Schnitt.
Und inniglich, der Zartheit voll
liebkost die Mutter Leben
und Kinderhand den Vogel,
indes der Wanderer den Berghang säumt
– der Transzendenz entgegen,
dem Goldeszauber in Vollendung.
Januar 2018